How do you determine scalar, vector, and parametric equations for the plane that passes through the points A(1,-2,0), B(1,-2,2), and C(0,3,2)?
1 Answer
Scalar (or cartesian) equation:
# 5x +y = 3 #
Vector equation:
# bb(ul r) * ( (-10), (-2),(0) ) = -6# , or,# ( (x), (y),(z) ) * ( (-10), (-2),(0) ) = -6#
Parametric equations:
# { (x=t), (y=3-5t), (z=0) :} #
Explanation:
We seek scalar, vector, and parametric equations for the plane that passes through the coordinates:
# A(1,-2,0)# ,#B(1,-2,2)# , and#C(0,3,2)#
Firstly, we have:
# bb(vec(AB)) = bb(vec(OB)) - bb(vec(OA)) = ( (1), (-2),(2) ) - ( (1), (-2),(0) ) = ( (0), (0),(2) ) #
# bb(vec(AC)) = bb(vec(OC)) - bb(vec(OA)) = ( (0), (3),(2) ) - ( (1), (-2),(0) ) = ( (-1), (5),(2) ) #
We can gain, a vector that is perpendicular to these vectors by taking their cross product. Thus we can gain a normal vector,
# bb(ul n) = bb(vec(AB)) bb(xx) bb(vec(AC)) #
# \ \ \ = ( (0), (0),(2) ) bb(xx) ( (-1), (5),(2) )#
# \ \ \ = | ( bb(ul hat i), bb(ul hat j), bb(ul hat k)), (0,0,2),(-1,5,2) |#
# \ \ \ = | (0,2),(5,2) | bb(ul hat i) - | (0,2),(-1,2) | bb(ul hat j) +| (0,0),(-1,5) | bb(ul hat k) #
# \ \ \ = (0-10) bb(ul hat i) - (0+2) bb(ul hat j) + (0-0) bb(ul hat k) #
# \ \ \ = -10 bb(ul hat i) - 2 bb(ul hat j) #
Having gained the normal vector we can now form the vector equation of the plane using the vector form
# \ \ \ \ \ bb(ul r) * ( (-10), (-2),(0) ) = ( (0), (3),(2) ) * ( (-10), (-2),(0) )#
# :. bb(ul r) * ( (-10), (-2),(0) ) = -6# , or,# ( (x), (y),(z) ) * ( (-10), (-2),(0) ) = -6#
Then if we evaluate the scalar product, we obtain the cartesian equation:
# (x)(-10) + (y)(-2) + (z)(0) = -6 #
# :. -10x -2y + 0 = -6 #
# :. 5x +y = 3 #
And we can parameterize by setting
# 5t+y=3 => y = 3-5t #
Thus the parametric equations are
# { (x=t), (y=3-5t), (z=0) :} #
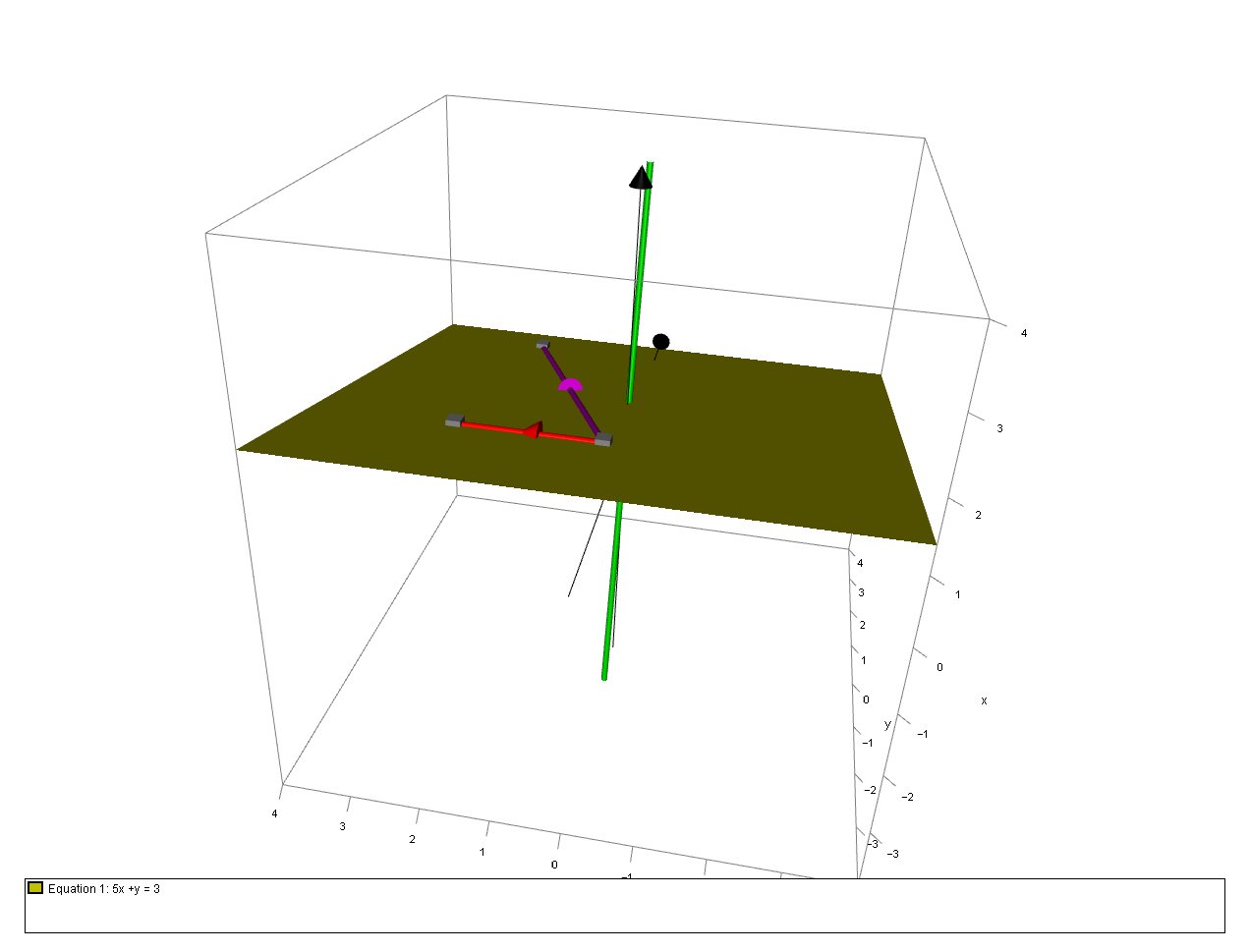
And, we can verify these results graphically: