19. "Describe the motion of a particle with position (x,y) as t varies in the given interval" ?
x=5+2\cos\color(maroon)(cancel(t))\pit , y=3+2\sin\pit , 1\let\le2
*thanks to Ultrilliam for pointing it out,
x=5+2\color(red)(\cos\pi\t)
*thanks to Ultrilliam for pointing it out,
2 Answers
See explanation
Explanation:
for
for
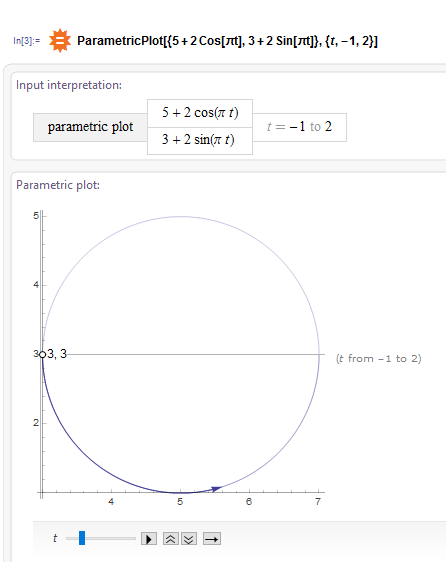
Based on Wolfram Alpha, the particle moves counterclockwise in a circular manner from (
 Slader
Slader
In cartesian: circle with centre
Period
Explanation:
Set it up for the Pytharorean identity like this:
-
x=5+2\cos\ \pi t implies cos pi t = (x-5)/2 -
y=3+2\sin\pi t implies sin pi t = (y - 3)/2
Pytharorean identity
-
sin^2 alpha + cos^2 alpha = 1 implies -
((x-5)/2)^2 + ((y - 3)/2)^2 = 1
Circular motion with centre
Remember that
So you can also describe the periodicity of the motion as
Finally, the interval:
-
((x(1)),(y(1))) = ((3),(3)) -
((x(2)),(y(2))) = ((7),(3))
From the graph, you can see that it's making the CCW journey along the bottom half of the circle in that time interval
graph{ (x-5)^2 + (y - 3)^2 = 2^2 [-10, 10, -5, 5]}


