Rose Curves
Key Questions
-
Answer:
The polar equation of a rose curve is either
#r = a cos ntheta or r = a sin ntheta# . The number of rose petals will be n or 2n according as n is an odd or an even integer. See explanation.Explanation:
Having seen that there were more than 1 K viewers in a day, I now add more.
The 2-D polar coordinates
#P ( r, theta)# , r =#sqrt (x^2 + y^2 ) >= 0# . It represents length of the position vector#< r, theta >. theta# determines the direction. It increases for anticlockwise motion of P about the pole O. For clockwise rotation, it decreases. Unlike r,#theta# admit negative values.r-negative tabular values can be used by artists only.
The polar equation of a rose curve is either
#r = a cos ntheta or r = a sin ntheta# .n is at your choice. Integer values 2,, 3, 4.. are preferred for easy counting of the number of petals, in a period. n = 1 gives 1-petal circle.
To be called a rose, n has to be sufficiently large and integer + a fraction, for images looking like a rose. For integer values, the petals might be redrawn, when the drawing is repeated over successive periods.
.
The period of both#sin ntheta and cos ntheta# is#2pi/n# .The number of petals for the period
#[0, 2pi/n]# will be n or 2n ( including r-negative n petals ) according as n is odd or even, for#0 <= theta <= 2pi# . Of course, I maintain that r is length#>=0# , and so non-negative. For Quantum Physicists, r > 0.Foe example, consider
#r = 2 sin 3theta# . The period is#2pi/3# and the number of petals will be 3. In continuous drawing. r-positive and r-negative petals are drawn alternately. When n is odd, r-negative petals are same as r-positive ones. So, the total count here is 3.Prepare a table for
#(r, theta)# , in one period#[0, 2pi/3]# , for#theta = 0, pi/12, 2pi/12, 3pi/12, ...8pi/12# . Join the points by smooth curves, befittingly. You get one petal. You ought to get the three petals for#0 <= theta <= 2pi.# .For
#r = cos 3theta# , the petals rotate through half-petal angle =#pi/6# , in the clockwise sense.A sample graph is made for
#r = 4 cos 6theta# , using the Cartesian
equivalent. It is r-positive 6-petal rose, for#0 <=theta <=2pi# .graph{(x^2+y^2)^3.5-4(x^6-15x^2y^2(x^2-y^2)-y^6)=0}
-
Answer:
#r = a sin(n theta) " or " r = a cos (n theta)# Explanation:
Given: A rose curve
#r = a sin(n theta) " or " r = a cos (n theta)# ,where
#a = "a constant that determines size"# and if
#n = "even"# you'll get#2n# petalsand if
#n = "odd"# you'll get#n# petalsTo graph a rose curve on a graphing calculator:
select MODE, arrow down to FUNC, arrow over to POL ENTER
select
#Y=# and enter the following:#r_1 = 8 sin 5 theta# GRAPH# => # graphs a 5 petaled rose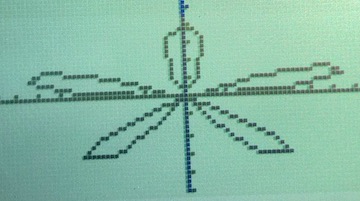
#r_1 = 8 sin 4 theta# GRAPH# => # graphs a 8 petaled rose
-
A rose curve has an equation of the form
#r=cos(n theta)# ,where
#n=1,2,3,...#
Examples
Odd:
#n=5# (5 petals)Even:
#n=4# (8 petals)Remark: As shown above, if
#n# is odd, then a rose has#n# petals, however, if#n# is even, then a rose has#2n# petals.
I hope that this was helpful.