Question

A wire in the shape of Y is hanged from two points `A` and `B`, `8` feet apart. The lower end of wire reaches a point `10` feet from `AB`. What is the shortest possible length of the wire?

Answer 1

Shortest length of wire that can be used is `12.31` feet.

Explanation:

The above can be better described by the following figure.

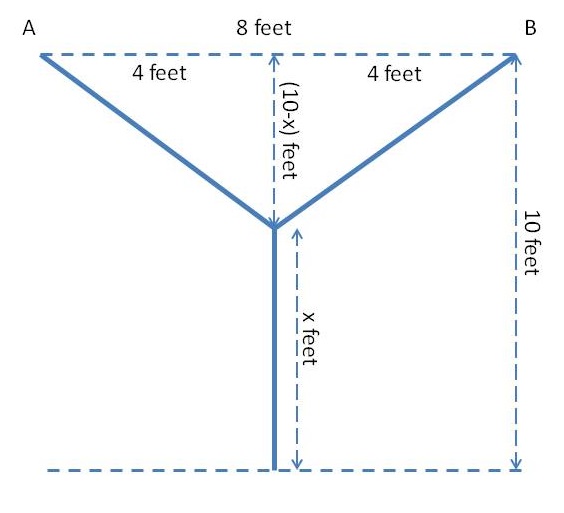
Now using Pythagoras theorem, if `x` is the length of verticle component of wire, lengths of tilted wires each is

`sqrt(4^2+(10-x)^2)` or `sqrt(16+100+x^2-20x)` or `sqrt(x^2-20x+116`

and total length of wire is `l(x)=x+2 sqrt(x^2-20x+116)`

This will be minimum when `(dl)/(dx)=0`

As `(dl)/(dx)=1+2xx1/(2sqrt(x^2-20x+116))xx(2x-20)=0`

or `1-(2(10-x))/sqrt(x^2-20x+116)=0`

or `sqrt(x^2-20x+116)=20-2x`

and squaring we get

`x^2-20x+116=400+4x^2-80x`

or `3x^2-60x+284=0`

or `x=(60+-sqrt(3600-4xx3xx284))/6`

`=(60+-sqrt(3600-3408))/6=(60+-sqrt192)/6`

or `x=10+-2.31` i.e. `x=12.31` or `7.69`

But `x` cannot be greater than `10`

Hence `x=7.69` and shortest length of wire that can be used is

`l(7.69)=7.69+2sqrt(7.69^2-20xx7.69+116)`

= `7.69+2sqrt21.3361=7.69+4.62=12.31`

Answer 2

The shortest total length of the wire that can be used `=16.92ft`

Explanation:

Let the length of the perpedicular `OD` dropped from the junction point `O` of Y-shaped wire frame to the horizontal line AB be `xft`.
The total height being 10ft the height of `O` will be `(10-x)ft`
Since in `DeltaAOB` `OA=OB`
Here `D` will be mid point of `AB` So `AD=BD=4ft`

By pythagoras theorem

`OA=OB=sqrt(x^2+4^2)`

So total length of the wire

`L=2sqrt(x^2+4^2)+10-x.....(1)`

To know the minimum length of wire required we impose the condtion `(dL)/(dx)=0`

So

`d/(dx)(2sqrt(x^2+4^2)+10-x)=0`

`=>(2*1/2*(2x)/sqrt(x^2+4^2)-1)=0`

`=>(2x)/sqrt(x^2+4^2)=1`

`=>(2x)^2=(sqrt(x^2+4^2))^2`

`=>4x^2=x^2+16`

`=>x=4/sqrt3`

Hence minimum length can be had by inserting `=>x=4/sqrt3` in (1)

`L_"min"=2(sqrt((4/sqrt3)^2+4^2))+10-4/sqrt3`

`=>L_"min"=2xx8/sqrt3+10-4/sqrt3`

`=>L_"min"=16/sqrt3-4/sqrt3+10`

`=>L_"min"=12/sqrt3+10=4sqrt3+10=16.92ft`