Question

What is the molecular electron configuration of `"F"_2`?

Answer 1

`(sigma_(2s))^2 (sigma_(2s)^"*")^2 (sigma_(2p_z))^2 (pi_(2p_x))^2 (pi_(2p_y))^2 (pi_(2p_x)^"*")^2 (pi_(2p_y)^"*")^2`

---

Recall that there are orbital mixing effects for homonuclear diatomic molecules that decrease from left to right until `"N"_2` (inclusive), which gives rise to a molecular orbital ordering of `(pi_(2p_x), pi_(2p_y))` and then `sigma_(2p_z)`, upwards. See here if you don't remember.

Notice how the `sigma_(g)(2p)`, or the `sigma_(2p_z)` molecular orbital, dips down below the `pi` molecular orbital energies after `"N"_2`.

Since `"F"_2` is after `"N"_2` in the second row of the periodic table (where these effects are not present), the orbital energy ordering is "normal".

In general, the molecular orbital energies follow these rules:

• The relative atomic orbital energy differences approximate the relative `sigma//sigma` orbital energy differences.

So, `sigma_(2s)` molecular orbitals are significantly lower in energy than `sigma_(2p_z)` molecular orbitals because the corresponding `2s` atomic orbitals are significantly lower in energy than the `2p`'s.

• `sigma` molecular orbitals are singly-degenerate, and `pi` molecular orbitals are doubly-degenerate.
• `sigma` molecular orbitals, in principle, get more stabilized upon overlap than `pi` molecular orbitals do.

For example, an `ns//ns` overlap for a homonuclear diatomic molecule gives rise to a partial MO diagram like this:

and an `np//np` overlap for `"O"_2` and `"F"_2` gives:

So, the full MO diagram is:

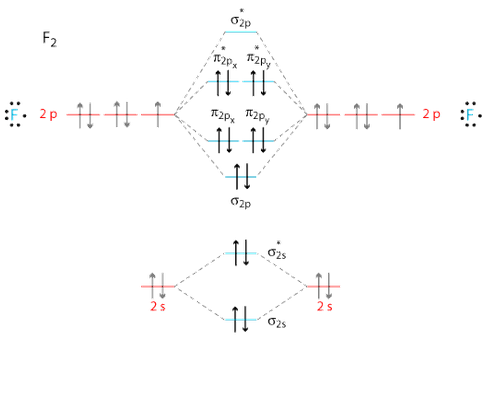
Thus, the valence electron configuration is:

`color(blue)((sigma_(2s))^2 (sigma_(2s)^"*")^2 (sigma_(2p_z))^2 (pi_(2p_x))^2 (pi_(2p_y))^2 (pi_(2p_x)^"*")^2 (pi_(2p_y)^"*")^2)`