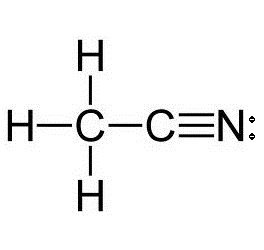
What is the hybridization of each carbon atom in acetonitrile?
1 Answer
Here's what I got.
Explanation:
Start by drawing the Lewis structure of acetonitrile,
The total number of valence electrons present in a molecule of acetonitrile will be equal to
# 2 xx "4 e"^(-) = "8 e"^(-) -># from two atoms of carbon,#"C"# #3 xx "1 e"^(-) = "3 e"^(-) -># from three atoms of hydrogen,#"H"# #1 xx "5 e"^(-) = "5 e"^(-) -># from one atom of nitrogen,#"N"#
Now, the two carbon atoms will be bonded together via a single bond. One of the two carbon atoms will be bonded to the nitrogen atom via a triple bond and the other will be bonded to the three hydrogen atoms via single bonds.
This will account for
#4 xx "2 e"^(-) + 1 xx "6 e"^(-) = "14 e"^(-)#
The remaining
In order to find the hybridization of the two carbon atoms, you must count the regions of electron density that surround the atoms.
A region of electron density is simply
- a single, double, or triple bond
- a lone pair of electrons
The number of regions of electron density will give you the steric number of the atom, which in turn will give you its hybridization.
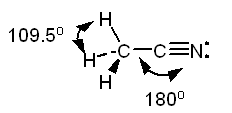
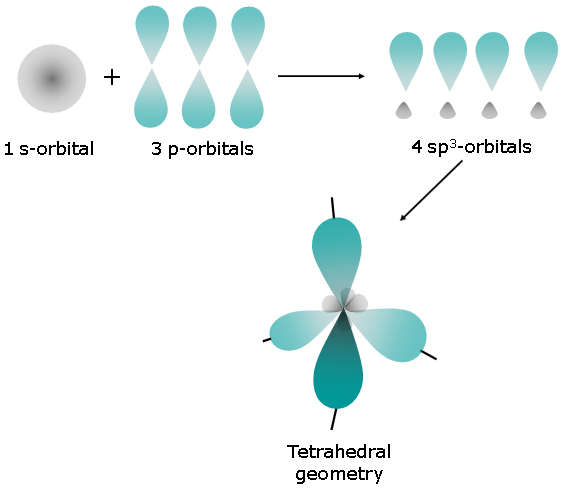
In this case, the left carbon atom is surrounded by
The steric number will be equal to
The right carbon is surrounded by
In this case, the steric number will be equal to
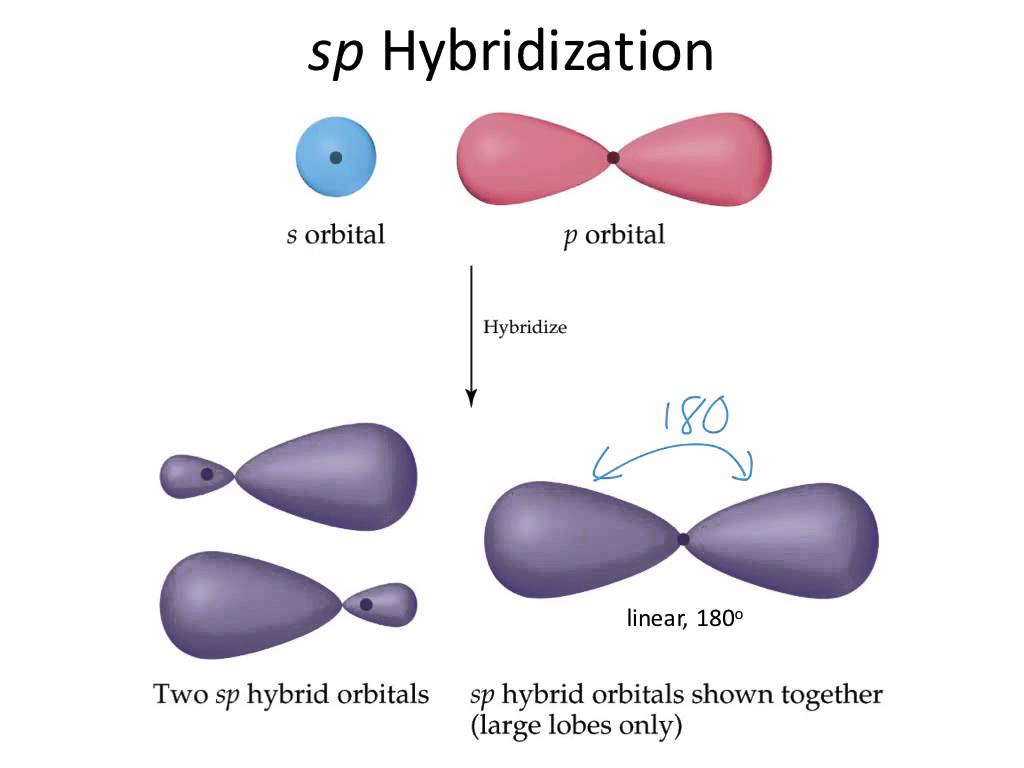
Consequently, the left carbon will have