Given a right triangle, let x be one of its acute angles. Suppose that the side opposite to angle x has length 15 and that the side adjacent to angle x has length 23. How do you find the approximate value of angle x in radians?
1 Answer
Start by drawing a diagram.
Explanation:
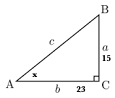
This is right angled trigonometry, so the technique to proceed is via SOHCAHTOA. First, out of
Here are the definitions:
-
-
-
These definitions are extremely important. They will serve you throughout your mathematical career in school. At the beginning, you can remember them with SOHCAHTOA, or Sin = opposite/hypotenuse, etc.
The next step in determining the value of
Now, we must set up a proportion.
Hopefully this helps!

