Question

Given an isosceles triangle with the tip is 110 degrees and two side are both 20 how do you find the base and the two angles by the base?

Answer 1

Here is a diagram.

Explanation:

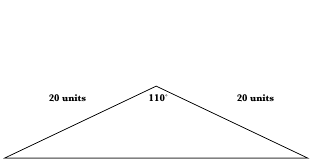
It is true that we could use Cosine's Rule to solve this triangle, but there is a much simpler method.

We know this triangle is isosceles. Therefore, the two angles we don't know have equal measures.

We can therefore state that `A + A + 110 = 180`, where A are the two angles we don't know. Solving:

`2A = 180 - 110`

`2A = 70`

`A = 35˚`

Hence, the two other angles measure `35˚` each.

Now that we know this vital information, we can cut this large triangle into two smaller triangles, as shows the next image.

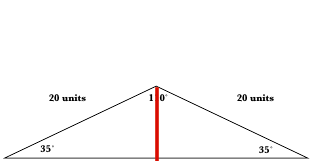
Since the triangle is isosceles, the angle that is made between the base and the red line (height) measures `90˚`. We can thus use SOHCAHTOA, or right angled trigonometry.

Also, note that the base has been perfectly cut into `2` pieces that measure equal lengths. Let these segments be `x`.

We know the hypotenuse and we want to know the side adjacent our angle (`35˚)`. We will therefore use cosine.

`x/20 = cos35˚/1`

`x = 20cos35˚`

`"length"_"base" = 2x`

`"length"_"base" = 2(20cos35˚)`

`"length"_"base"= "32.77 units"`

Hence, the base measures 32.77 units.

Hopefully this helps!