How do you draw a newman projection of the most stable conformation of 2R,3S-dibromobutane sighting down the #C_2-C_3# bond? Is this optically active, racemic, dextrorotatory, or a meso compound?
1 Answer
Based on the name, I've drawn out the structure like this:
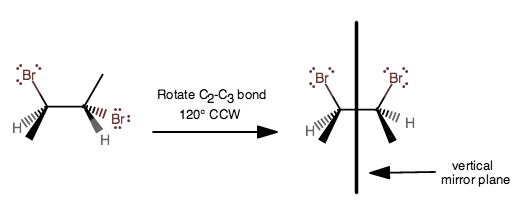
Rotating the
Although both carbon 2 and carbon 3 are chiral carbons, their optical activities cancel out (they rotate plane-polarized light to the same extent in opposite directions), so there no net optical activity for this meso compound.
To make the Newman projection, it helps to progress to a Sawhorse projection, and that should help you see where you can go to condense the structure down into the Newman projection.
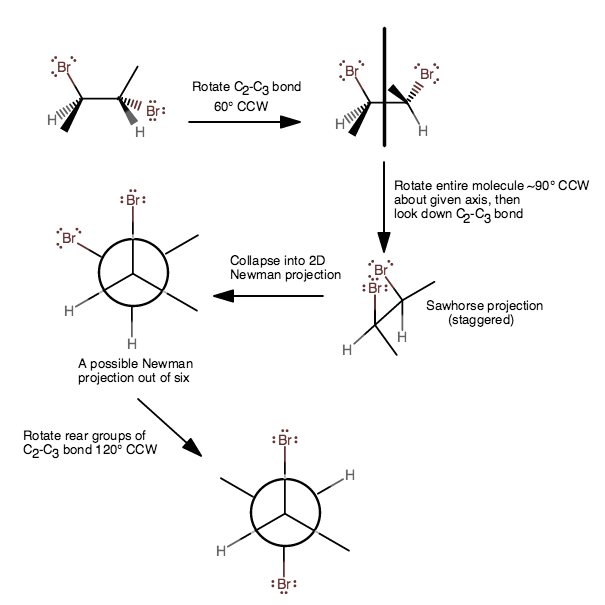
1) From the first, left structure, rotate the
2) Then rotate the entire molecule along the axis (depicted in the image directly above) that is coplanar with the mirror plane approximately
3) Then, it can be condensed into the Newman projection fairly easily if it's already oriented; try picturing yourself squishing the
Now is this the most stable one? The most stable one would have the rear hydrogen in between the front methyl and bromine in a staggered conformation to minimize [lone-pair]-[bonding-electron] repulsions.
4) Rotate the rear groups on the
CHALLENGE: Can you draw out the other four Newman projections? Three are eclipsed conformations, and the last one is the third staggered conformation that I didn't show.

