How do you find parametric equation for given curve #y²=4ax#?
1 Answer
Oct 15, 2016
#y^2=4ax#
Center
Focus
Directrix
Explanation:
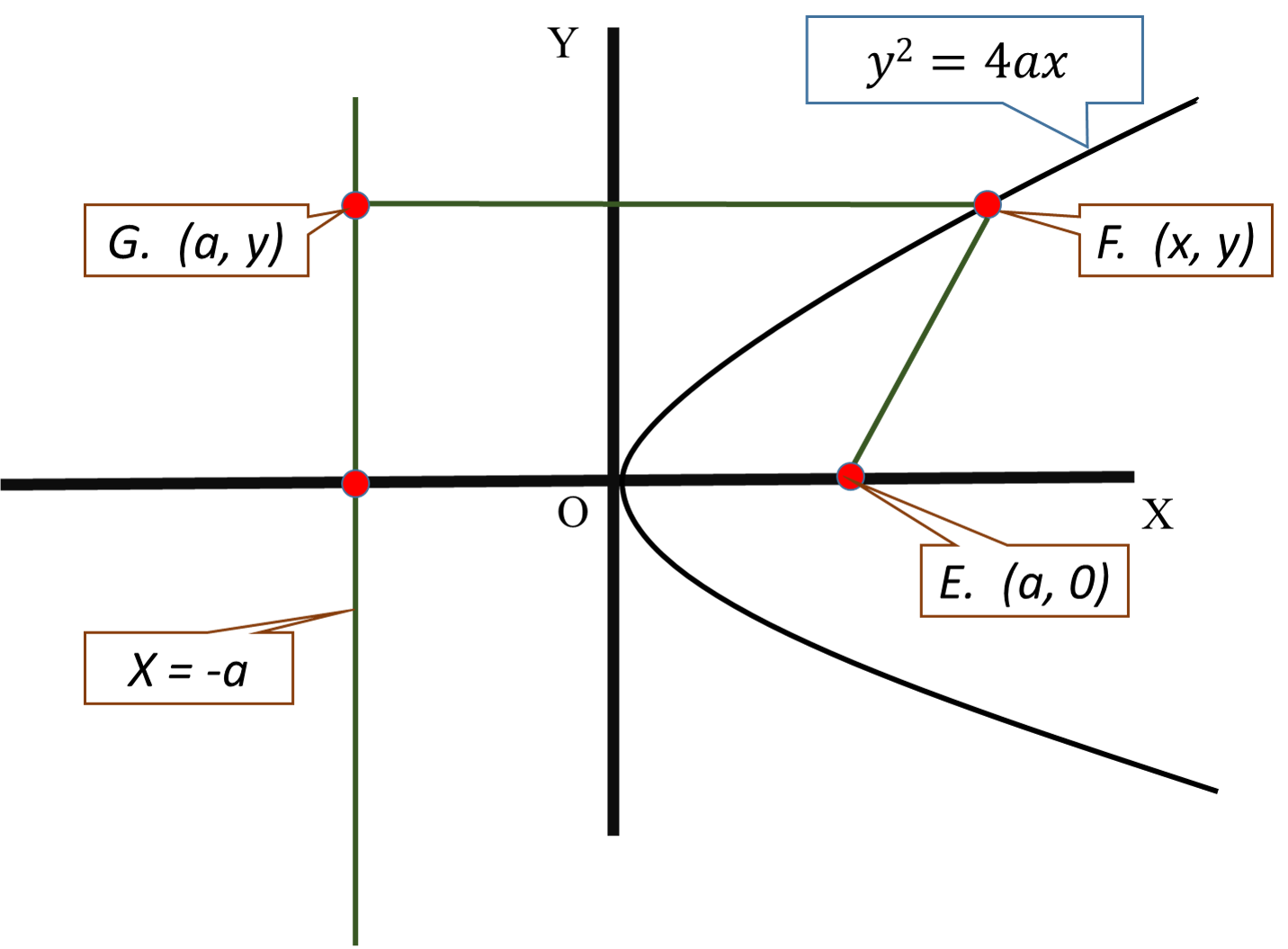
The parabola's center is
It is focus is at point E
Its directrix is
Take any point on the parabola. in our case it is F.
The coordinates are
Then -
#(x-a)^2+(y-0)^2=(x-(-a))^2+(y-y)^2#
The Distance between E and F is equal to the distance between F and G.
#(x-a)^2+(y-0)^2=(x+a)^2+(y-y)^2#
#x^2-2ax+a^2+y^2=x^2+2ax+a^2#
#cancel(x^2)-2ax+cancel(a^2)+y^2=cancel(x^2)+2ax+cancel(a^2)#
#y^2=2ax+2ax#
#y^2=4ax#
Center
Focus
Directrix