How do you graph #r=2sintheta#?
1 Answer
Apr 8, 2018
Please see below.
Explanation:
As
Thus these represents points
We can select more such points, say by having
The gaph will appear as follows:
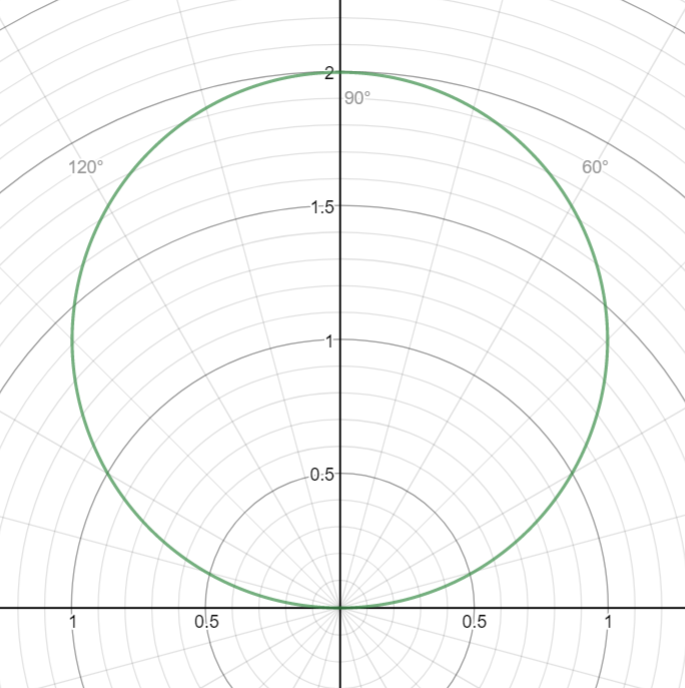
It is a circle with center at
and as
in rectangular coordinates, it is equivalent to
