Question

How do you sketch the graph that satisfies f'(x)>0 when x<3, f'(x)<0 when x>3#, and f(3)=5?

Answer 1

We know the following.

•The function is increasing in the interval `(-oo, 3)`

•The function is decreasing in the interval `(3, oo)`

•The function passes through the point `(3, 5)`

Considering the function is exclusively increasing in the interval `(-oo, 3)` and exclusively decreasing `(3, oo)`, then `(3, 5)` must be a maximum.

Any polynomial function of the form `-a(x + 3)^n + 5`, where `n` is an even integer and , would satisfy the requirements given in the function.

The following is a graph of `-2(x + 3)^6 + 5`, which satisfies perfectly the requirements of your question.

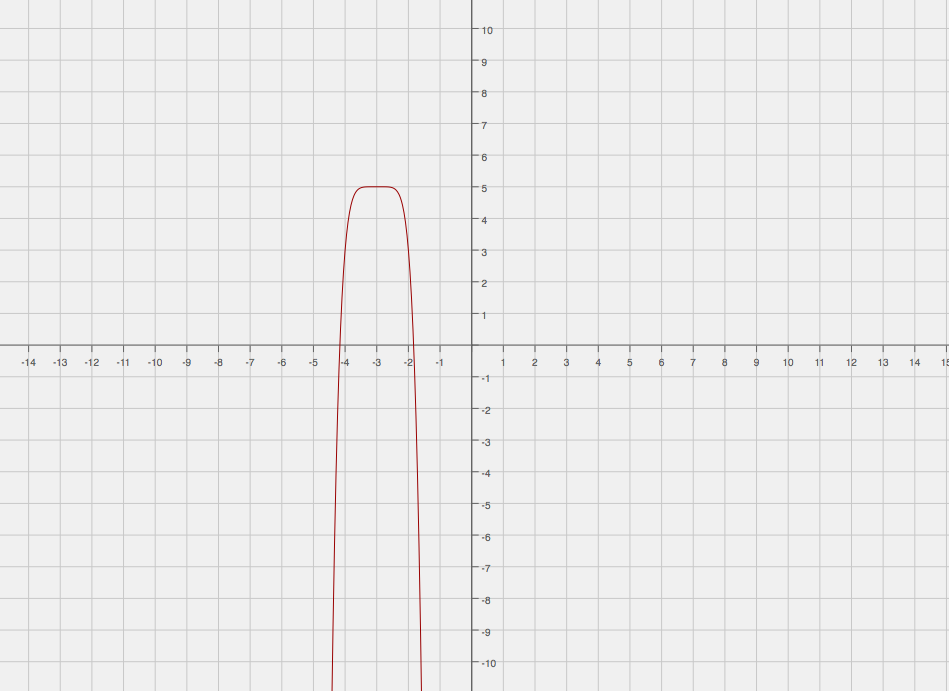
Hopefully this helps!

Answer 2

Here are a couple more possibilities.

Explanation:

HSBC244 has shown a nice graph that has derivative `f'(3)=0`.

Here are couple of graphs of functions that satisfy the requirements, but are not differentiable at `3`.

`f(x) = -abs(x-3)+5` is shown below.

graph{y = -abs(x-3)+5 [-14, 22.05, -6.16, 11.85]}

`f(x) = -(x-3)^(2/3) +5` is shown on the next graph.

graph{-(x-3)^(2/3) +5 [-5.98, 14.025, -2.15, 7.844]}

For the unconventional here is a possible graph:

`f(x) = {(-(x-3)^2+1," if ",x < 3),(5," if ",x = 3),(-x+6," if ",3 < x) :}`

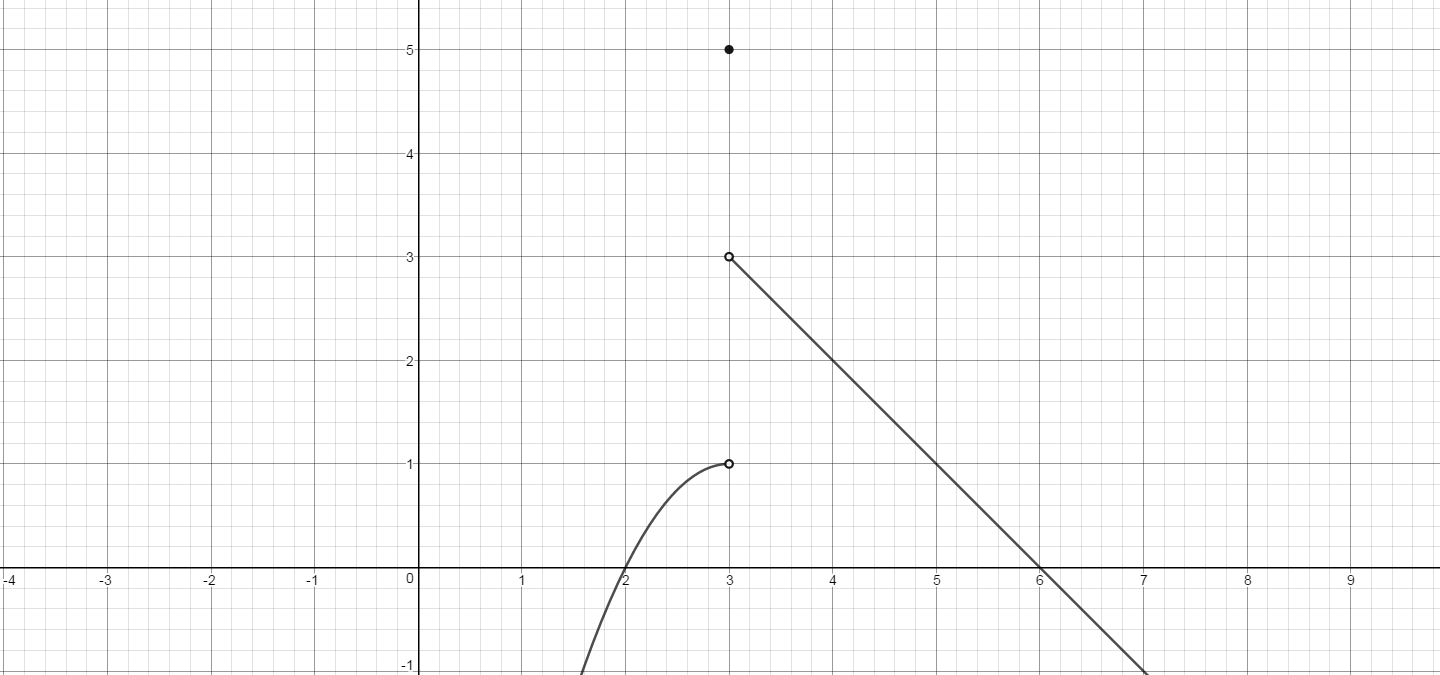
(Graphed using desmos.com)