Question

How do you solve a right triangle with side B = 46° and side c = 30 feet?

Answer 1

First, draw a diagram to represent the situation.

Explanation:

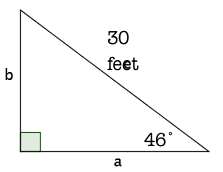
As you can see, we are looking for two sides and one angle. Let's do the simplest task first, which is to find angle A.

A= 180˚ - 90˚ - 46˚

A = 44˚

Now we can use the primary trigonometric ratios to find sides a and b.

Starting with b:

`b/30` = `sin46/1`

Solve for b -->b = 21.58

Finishing with a:

`a/30` = `cos46/1`

a = 20.84

So, A = 44˚, a = 20.84 feet and b = 21.58 feet

Hopefully this helps. Below I have included a few exercises for you to practice yourself with should you choose to practise more.

1. Solve the following triangles:

a) ∆ABC where A = 56˚ and c = 24 inches

b) ∆ABC where b = 35 cm and c = 27 cm.

1. A photographer is standing 34 meters from a skyscraper, and the angle of elevation between him [the photographer] and the top of the building is 65˚. Find the height of the building rounded to two decimals