Question

How do you translate a graph up or down?

Answer 1

You can translate any function, `y=f(x)` using:

`y=f(x-h)+k` or
`y-k=f(x-h)`

If `h` is positive, the graph will translate to the right.
If `h` is negative, the graph will translate to the left.
If `k` is positive, the graph will translate up.
If `k` is negative, the graph will translate down.

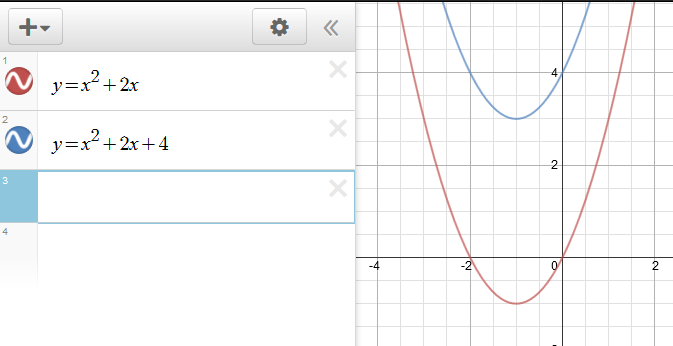
Here is an example:

`f(x)=x^2+2x`

If we want to translate this up 4 units, then we have:

`y=f(x)+4`
`y=x^2+2x+4`

If we have a different example:

`f(x)=1/x`
`y=f(x)+4`
`y=1/x+4`

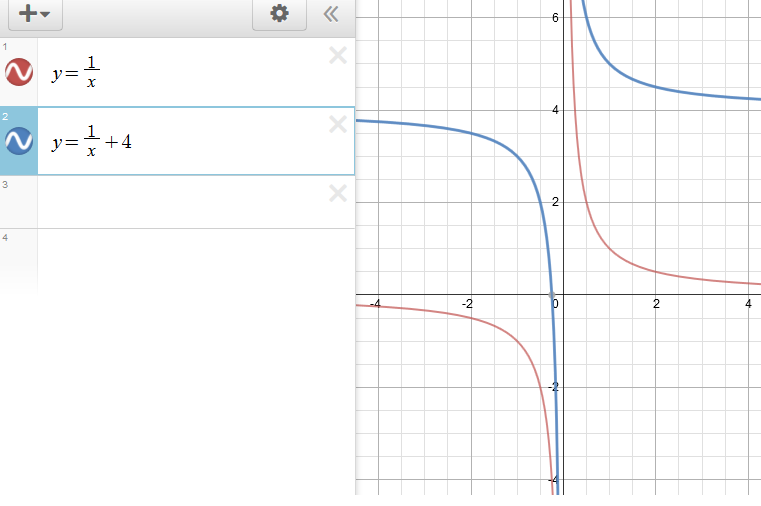
It still works!