Translation of a Conic Section
Key Questions
-
When translating a graph to the left or to the right, it means moving the entire graph to the left or to the right of its current location, which is usually relative to
#(0, 0 )# For example, let's say you have a circle centered at
#(0, 0)# with radius 2. Its standard equation would be#x^2 + y^2 = 4# Now, let's say we translate the circle 5 units to the left. Your circle will now be centered at (-5, 0) with the radius still equal to 2. Its new standard equation would be
#(x + 5)^2 + y^2 = 0#
This is also true for linear equations.
For example, let's say you have a line with slope 1 with the x-intercept equal to 0. Its equation will be#y = x# When we translate the line 3 units to the right, its slope will remain the same, but its x-intercept will now be 3. Its new equation will be
#y = x - 5# 
seph
·
2
·
Oct 25 2014
-
Translations are simply horizontal and/or vertical shifts. So,
#y = sqrtx - 2# is shifted 2 units down from#y = sqrtx# , while#y = sqrt(x-2)# is shifted 2 units right of#y = sqrtx# .#y = sqrtx# :
graph{sqrtx [-10, 10, -5, 5]}#y = sqrtx - 2# :
graph{sqrtx - 2 [-10, 10, -5, 5]}#y = sqrt(x - 2)# :
graph{sqrt(x-2) [-10, 10, -5, 5]}#y = sqrt(x - 2) - 2# :
graph{sqrt(x-2) - 2 [-10, 10, -5, 5]}
Truong-Son N.
·
1
·
Jun 12 2015
-
You can translate any function,
#y=f(x)# using:#y=f(x-h)+k# or
#y-k=f(x-h)# If
#h# is positive, the graph will translate to the right.
If#h# is negative, the graph will translate to the left.
If#k# is positive, the graph will translate up.
If#k# is negative, the graph will translate down.Here is an example:
#f(x)=x^2+2x# If we want to translate this up 4 units, then we have:
#y=f(x)+4#
#y=x^2+2x+4#
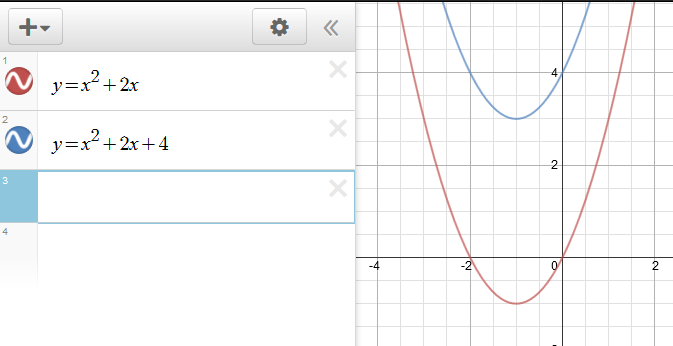
If we have a different example:
#f(x)=1/x#
#y=f(x)+4#
#y=1/x+4#
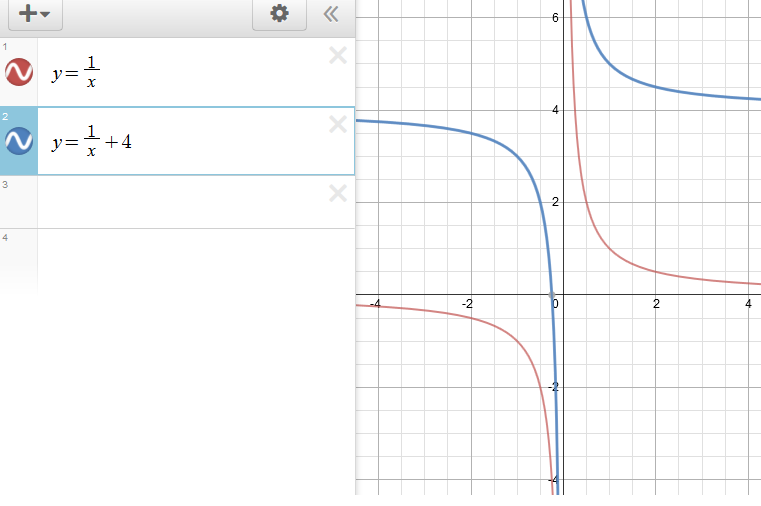
It still works!
Amory W.
·
·
Sep 22 2014