The legs of a right triangle are 5cm and 12 cm long. How do you find the lengths, to the nearest tenth, of the segments into which the bisector of the right angle divides the hypotenuse?

Question

11915 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-11-03T22:48:55

Draw a sketch, then use the Law of Sines

Here is a sketch of the problem:

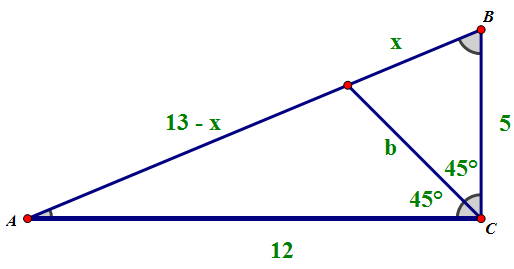
enter image source here

Using Pythagorean theorem, we know the hypotenuse length of #Delta ABC# is 13. So the two segment lengths can be labeled (13-x) and x.

We also know:
#/_A=tan^-1(5/12)#
#/_B=tan^-1(12/5)#

Now use the Law of Sines:

#(sin45)/x=(sin(tan^-1(12/5))/b)#
#(sin45)/(13-x)=(sin(tan^-1(5/12))/b)#

Next, divide the first equation above by the second equation so that both #sin45# and b cancel out.

You will be left with the following identity:

#(13-x)/(x)=(sin(tan^-1(12/5)))/(sin(tan^-1(5/12)))#

Solving for x and (13-x):
#x=3.8#
#13-x=9.2#

Hope that helped