Question

A flagpole sits on the top of a building. Angles of elevation are measured from a point `500` feet away from the building. The angle of elevation to the top of the building is `38˚` and to the top of the flagpole `42˚`. How high is the flagpole?

Answer 1

The height of the flagpole is approximately `60` feet.

Explanation:

Always try to draw a diagram.

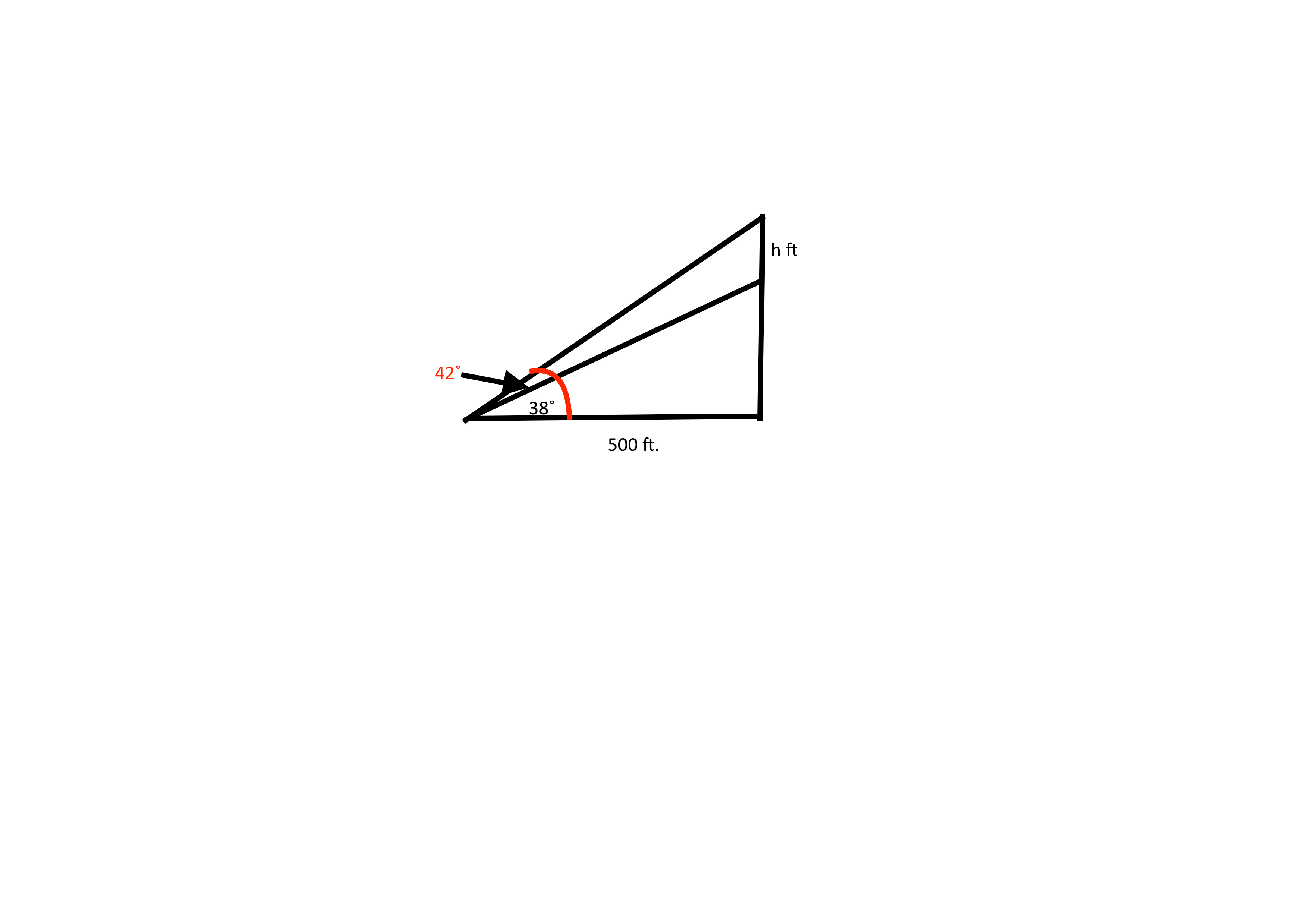
We know that there is a right angle between the ground and the building. Therefore, we can use the 3 basic trig ratios instead of the sine or cosine law to solve this problem.

Since the angle in the corner of the larger right triangle measures `42˚`, the top angle in this triangle measures `180˚ - 90˚ - 42˚ = 48˚`.

By basic trig ratios, we can find the height of the building with the flag pole on top, call it `H`.

`(tan42˚)/1 = H/500`

`H = 500tan42˚`

I would keep it in exact form until the last step.

We now devise an expression for the height of the building (without the flag pole). Call it `a`

`(tan38˚)/1 = a/500`

`a = 500tan38˚`

We can now state that

`h = H - a`

`h = 500tan42˚ - 500tan38˚`

`h ~~ 59.559 ~~ 60 "feet"`

Hopefully this helps!

Answer 2

The flagpole is `60ft` in height to the nearest foot.

Explanation:

1) The flagpole is on top of a building.
2)Angles of elevation both measured from point `500ft` from building
3) Angle of elevation to the top of building is `38deg`
4) Angle of elevation to the top of flagpole is `42deg`

The information above will provide us with two right angle triangles, one smaller one inside a larger one.

Both will have a base of `500ft`.

The smaller triangle will have a base angle `beta` of `38`deg opposite the `90`deg, and the larger triangle will have a base angle `beta` of `42`deg.

From this information we can find the heights of the building and the building + pole using the definition of the tangent of the two base angles `beta`:

`tan(beta)=(opp)/(adj)` where the `opp` is the height and the `adj` is the `500ft`

`opp(build)=tan(38)*(500ft)=390.6ft=`height of building

`opp(flag)=tan(42)*(500ft)=450.2ft=`height of building + pole

Then to the nearest foot the height of the flagpole is:

`450.2ft-390.6ft=60ft`