Question

How do you write the equation of the parabola in vertex form given vertex at (10, 0) and a directrix x = -2?

Answer 1

`y^2=48(x-10)`

Explanation:

As the vertex is `(10,0)` and directrix is `x=-2`, the distance of vertex from directrix is `10+2=12` and as vertex is to the right of directrix, focus will be further to the right of vertex by a distance of `12` units. Hence, focus is `(22,0)`.

Now parabola is the locus of a point `(x,y)`, whose distance from focus, which is `(22,0)` and directrix `x+2=0` is always same.

As distance from directrix is `|x+2}` and from focus is `sqrt((x-22)^2+y^2)`. As such equation of parabola is

`(x-22)^2+y^2=(x+2)^2`

or `x^2-44x+484+y^2=x^2+4x+4`

or `y^2=48x-480=48(x-10)`

graph{(y^2-48x+480)(x+2)((x-10)^2+y^2-0.2)((x-22)^2+y^2-0.2)=0 [-30.33, 49.67, -18.08, 21.92]}

Answer 2

`y^2=48(x-10)`

Explanation:

Look at the diagram -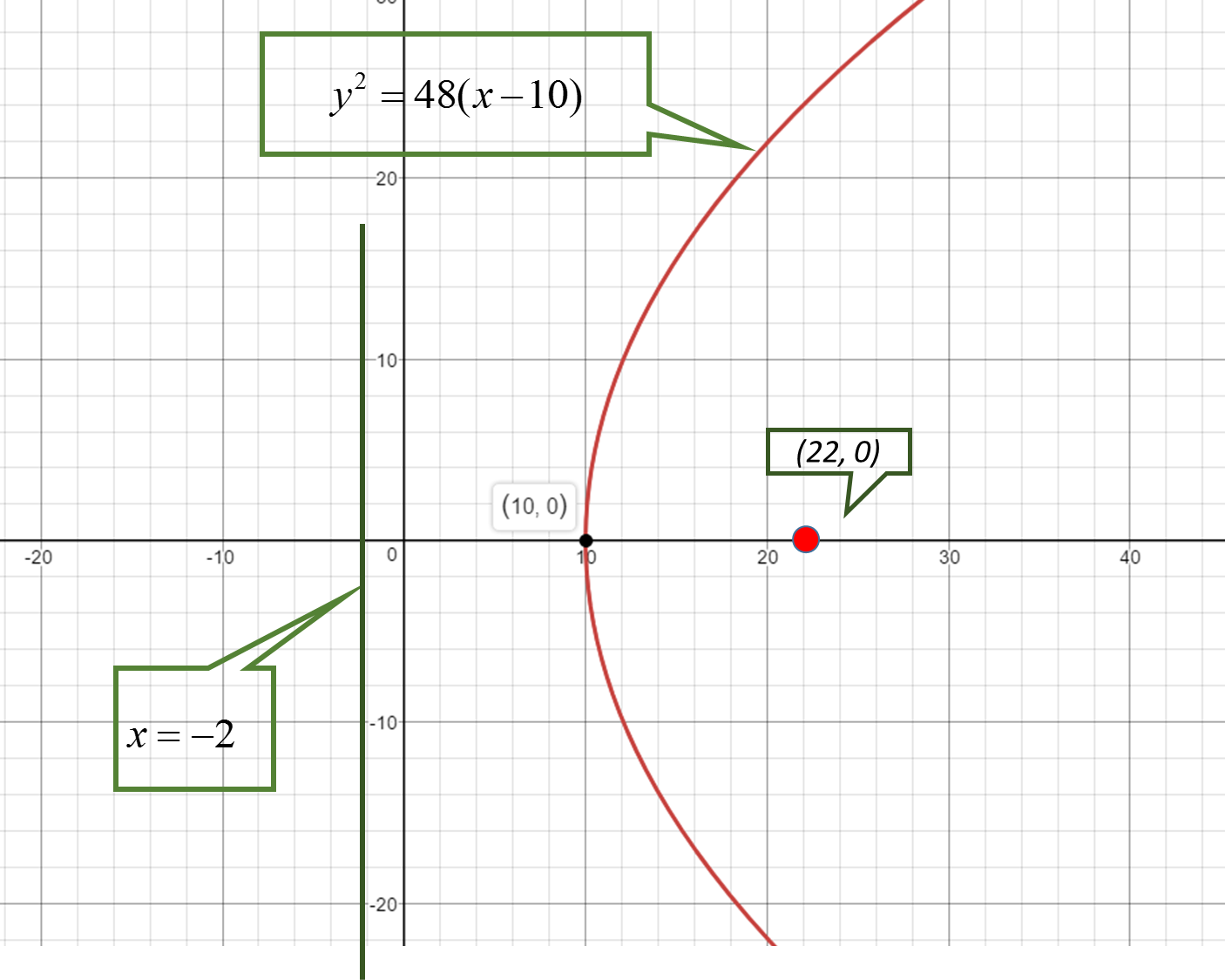

The curve opens to the right, hence its equation is -

`(y-k)^2=4xxaxx(x-h)`

Where-

`h=10` - x-coordinate of the vertex
`k=0` - y-coordinate of the vertex.
`a=12` - distance from the vertex to focus.

`(y-0)^2=4 xx 12xx(x-10)`

`y^2=48(x-10)`