We have a triangle that looks like:
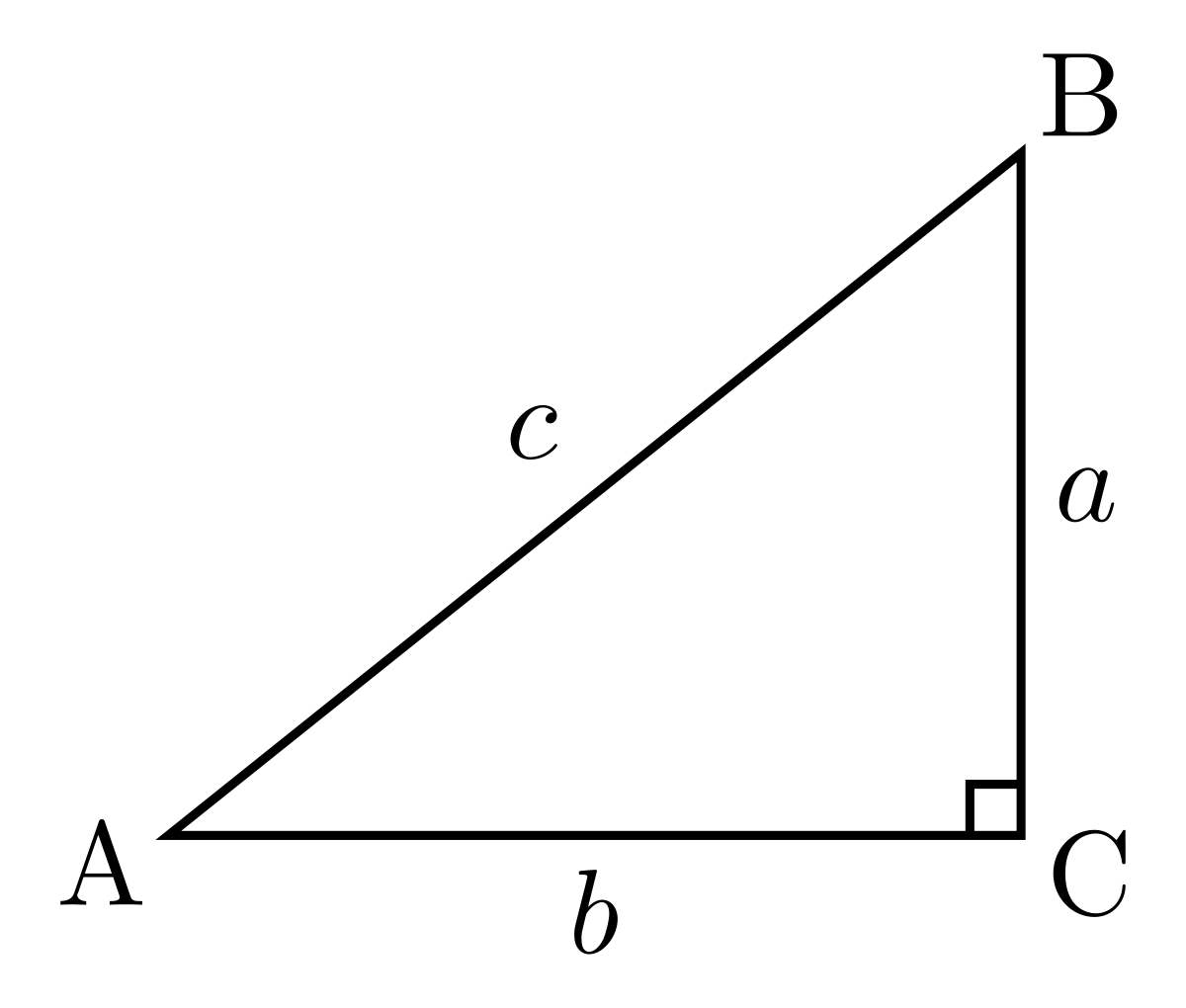
Here, we have that the angle #C=pi/2#, #b=16"units"# and angle #A=pi/12#.
Since all the angles of a triangle add up to #pi#, angle #B=(5pi)/12#.
According to the sine rule:
#sinA/a=sinB/b#
We have to solve for #a#. Inputting:
#(sin(pi/12))/a=(sin((5pi)/12))/16#
#a=(16*sin(pi/12))/(sin((5pi)/12))#
#a=4.287"units"#
Now there exist possibilities all around. There are a multitude of ways to solve for the area. Let's look at the two main ways of action.
- Take #a# as the height of the triangle and #b# the base, and use the formula #1/2bh# to solve for the area.
- Find #c# and use Heron's Formula to solve for the area.
Just for kicks, let's do both!
Use Method Number 1:
#A=1/2bh#
#A=1/2*16*4.29#
#A=34.297"units"^2#
Use Method Number Two:
We must find #c# first. To do this, too, we have two methods:
Again, for kicks, I'm doing both.
#color(white)(oleoleole)#Sub-method Number 1:
#color(white)(oleoleole)#We have the Pythagoras' Theorem #a^2+b^2=c^2#.
#color(white)(oleoleole)#We also know that #a=4.29, b=16#. Inputting:
#color(white)(oleoleole)##16^2+4.29^2=c^2#
#color(white)(oleoleole)##c^2=274.404#
#color(white)(oleoleole)##c=16.565"units"#
Now for:
#color(white)(oleoleole)#Sub-Method Number 2
#color(white)(oleoleole)#We have the cosine rule: #c^2=a^2+b^2-2abcosC#
#color(white)(oleoleole)#We know the stuff we stated above, and #color(white)(oleoleole)#that #C=pi/2#
#color(white)(oleoleole)#Since #cos(pi/2)=0#, the cosine rule #color(white)(oleoleole)##color(white)(oleoleole)#reduces to the Pythagoras' Theorem, which we #color(white)(oleoleole)#solved above, so skip it.
Now we go back to using Heron's Formula:
#A=sqrt(s(s-a)(s-b)(s-c))#, where #s=(a+b+c)/2#
Here, #a=4.287, b=16, c=16.565#. So:
#s=(4.287+16+16.565)/2#
#s=18.426#. Inputting all of that into Heron's Formula:
#A=sqrt(18.426(18.426-4.287)(18.426-16)(18.426-16.565))#
#A=sqrt(1176.216)#
#A=34.297"units"^2#
Two different methods, same answer!


