Find the coordinate of the vertices foci, end points of the minor axis, center, latus recta, the equation of the directrices, sketch the equation of #x^2+9y^2-24x-54y+51=0#?
1 Answer
We know that this equation defines an ellipse, since it has the squared terms added together for both. Similarly, we know it is in line with the axes since there is no cross term of
So we can factor by completing the square:
or in a more familiar form,
Vertices
This means that the major axis is in the
Foci
We see the two axial lengths:
so the foci are at
End Points of the Minor Axis
This means that the minor axis is in the
Center
The center is just
Latus Recta
The latus recta go through the foci and intersect the graph. We know that the
where the two
Directricies
The directrices will be vertical lines a distance of
Sketch
From all this, we can very clearly sketch the equation:
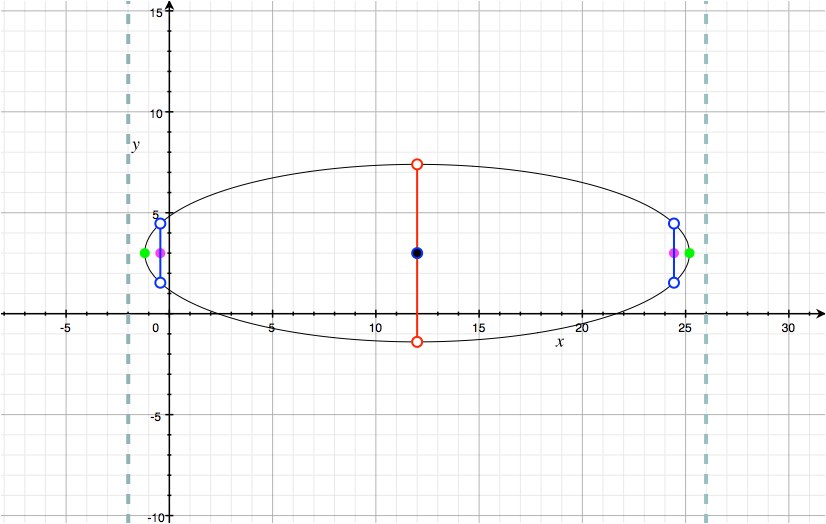
where the vertices are green, the foci are magenta, the minor axis is red, the center is black, the latus recta are blue, and the directricies are a muted cyan.
