Question

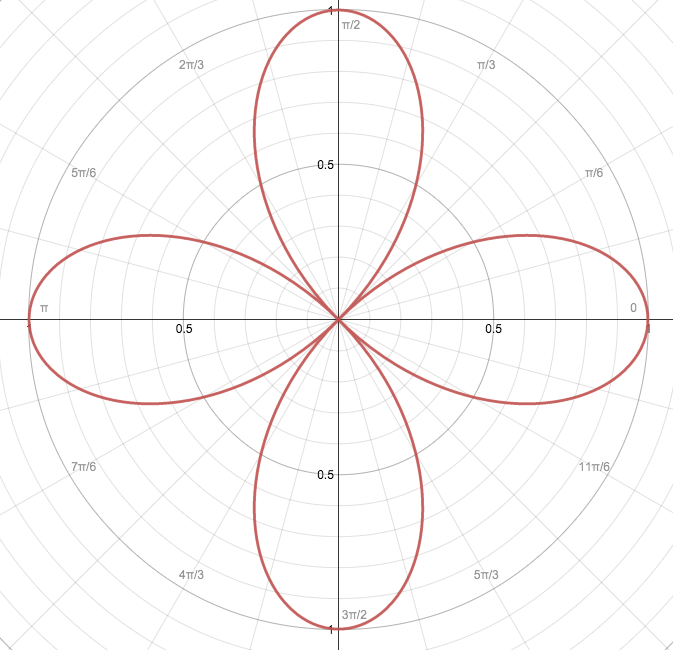
How do you graph the polar equation `r=cos2theta`?

Answer 1

Please see below.

Explanation:

The equation `r=cos2theta` is in polar coordinates.

When `theta=0,pi/2,pi,(3pi)/2,2pi`, we have `r=1`

and when `theta=pi/4,(3pi)/4,(5pi)/4,(7pi)/4`, we have `r=0`

Hence, the courve moves from `r=1` at `theta=0` to `r=0` at `theta=pi/4` to `r=1` at `theta=pi/2`. Note that in between at `theta=pi/6` we have `r=1/2` and so on forming four petals. That is why it is called rose curve as well.

The shape appears as shown below.