How do you represent electron orbitals through drawings?
2 Answers
Briefly, drawings reflect the probability density distribution for the wave function outputs for a specific orbital with quantum numbers
Explanation:
Each "drawing" is the probability density of the wave function for each respective sub-shell in a 3d plane.
Firstly, we have four quantum numbers:
For instance, the 2p subshell (
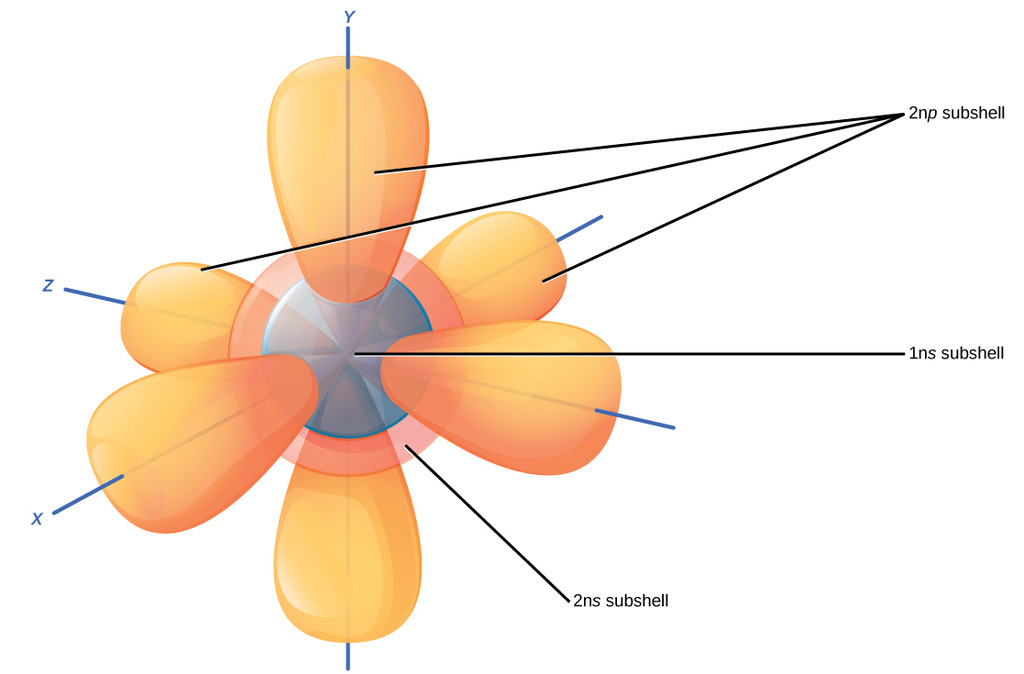
This picture at first seems like a giant, confusing mess. But let's tear it apart. It's merely the 1s, 2s, and 2p subshells for an atom. All of these are where electrons can be located in that atom, for instance this could be
Each of these orbitals in an
To extrapolate, a 3s subshell would merely be a sphere covering all of these orbitals, with two more electrons, and so on.
I assume you mean in an electron configuration, rather than an actual sketch of the orbitals. They could be represented through horizontal lines, and the electrons through arrows.
The
#ul(color(white)(uarr darr))#
#1s#
When half-filled, it could be represented as:
#ul(uarr color(white)(darr))#
#1s#
And when filled:
#ul(uarr darr)#
#1s#
Any other orbital can be represented in this way, and the higher up they are (relative to each other), the higher in energy they are.
The
Being in the same orbital gives two electrons the same principal quantum number
Therefore, no two electrons can have the same spin in the same orbital.


