General Solutions of Triangles
Key Questions
-
Answer:
Here is a view of methods to solve oblique (non-right) triangles.
Explanation:
Solving oblique triangles involves looking at what information you're given and either applying the Law of Sines or the Law of Cosines to solve the triangle.
The law of sines is
#sinA/a = sinB/b = sinC/c# in triangle ABC, while the law of cosines states that#a^2 = b^2 + c^2 - 2(bc)cosA# .When do we use Law of Sines?
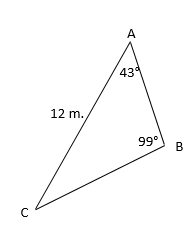
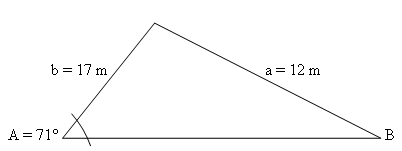 Warning: the angle-side-side case risks to be an ambiguous case: 0, 1 or 2 solutions possible
Warning: the angle-side-side case risks to be an ambiguous case: 0, 1 or 2 solutions possible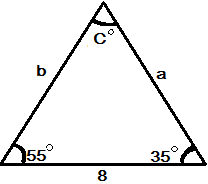
When do we use Law of Cosines?
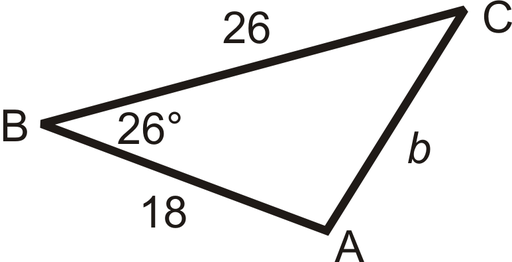
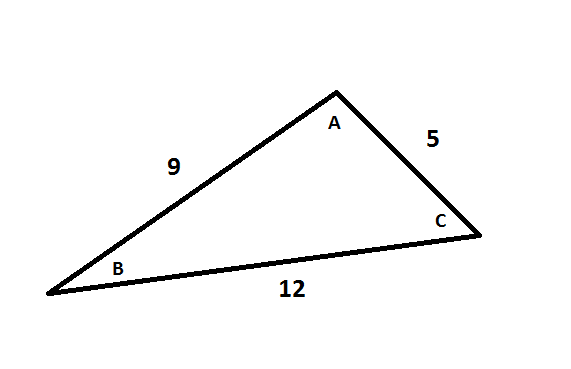
Hopefully this helps!
-
To use Pythagoras you must have a right angle triangle and know two of the sides. You use it to find the missing side.
To use the trig ratios {SOHCAHTOA} again you must have a right angled triangle and you use two sides to find an angle or an angle and a side to find the second side.
To use the Sine rule, in non right angled triangles you can find a missing side if you have a side and its corresponding angle plus the angle for the side you are finding. You can find an angle if you have its corresponding side plus another side with its corresponding angle.
to use the cosine rule again in non right angled triangles given two sides and the included angle you can find the third side. Or given all three sides you can find an angle.