Make the internet a better place to learn
During the fusion process, how is mass converted into energy?

Answer:
Explanation:
This is calculated using the famous equation of Einstein,
#E = m c^2#
In Fusion reaction like the ones taking place in the core of a Star, there is enough pressure to fuse hydrogen nuclei to form one helium nucleus.
So, 4 hydrogen nuclei are fused together to form one Helium nucleus. But, where does the energy come from that keeps the Sun from collapsing?.
When 4 Hydrogen nuclei are merged together they show a certain discrepancy in the mass when a Helium atom is formed, i.e the mass of 4 Hydrogen atoms before Fusion is higher than the mass of the Helium atom after the reaction this mass defect is converted into energy by
#"mass of a hydrogen atom " = " 1.00794 u"#
#"mass of one helium atom " = " 4.002602 u"#
Where
The mass defect,
#Delta m = 4 xx m_H - m_(He)#
#= 4 xx "1.00794 u" - "4.002602 u"#
# = "0.029158 u "# or#" "4.8416859 * 10^(-29)"kg"#
In the equation
This means that you have
#E = 4.8416859 * 10^(-29)"kg" * (3 * 10^8)^2"m"^2"s"^(-2)#
#E = 4.35751731 * 10^(-12)" J per reaction"#
Once a photon of light is generated, how long does it take to escape beyond the outer part of the Sun?

Answer:
It takes thousands of years for a photon to get from the sun's core to escape from the surface.
Explanation:
When a photon is created in the core of the sun it will collide with many protons and electrons in its path to the surface.
The photon effectively has to find a path to the surface by randomly being absorbed and re-emitted by particles on the way. This is an example of the drunkard's walk problem.
The number of steps, between particles on the way
Putting
The time taken for each step is
This gives a total time
This calculation assumes that the free mean step is actually about a centimetre, it could be much smaller, which would make the time longer. In any case it takes thousands of years to make the journey.
What fills space between galaxies?
Answer:
Mostly nothing but....
Explanation:

In between galaxies, it is mostly just empty space. And by empty, I don't mean the kind of empty in an empty jar but empty as in a vacuum - an area with no particles or atoms at all. However, there are a few "rogue stars". These lonely stars are not part of a larger body (galaxy), but sit on their own in space.
There is something else that fills space, but whether it counts as anything depends on what you class as something. I am, of course, talking about dark matter.
Physicists have found that there is not enough mass in the detectable universe to account for certain phenomena (e.g. there are galaxies that spin so fast that their observable mass couldn't possibly keep them together - there must be some mysterious form of mass that is contributing to it).
We don't really know anything about dark matter. It doesn't interact with the electromagnetic force, so we can't look at light or heat to discover more. Instead, we sort of just give it a label to account for it and sit rather puzzled.
It is worth mentioning this Dark Matter though, as it is thought to make up around 83% of the universe (or about 91% including dark energy).
For more on dark matter and rogue stars, here are two very interesting websites:
http://home.cern/about/physics/dark-matter
http://www.sciencemag.org/news/2014/11/rogue-stars-outside-galaxies-may-be-everywhere
I hope this helps; let me know if I can do anything else:)
Do black holes defy the laws of physics?

Answer:
Black holes challenge the laws of physics as we know them.
Explanation:
Nothing should be able to defy the laws of physics. If something is inconsistent with the laws of physics then they need to be modified to accommodate the inconsistency.
Black holes are extreme objects. They were predicted from the Schwarzschild solution to Einstein's General Theory of Relativity. Many people didn't think that they existed until evidence was found. A black hole could explain the galactic X-ray source at Cygnus X-1. It is now believed that most large galaxies have a supermassive black hole at their centres.
One issue with black holes is that the theories suggest that there is a singularity inside them. A singularity is a point of infinite density and infinite curvature of spacetime. The physicist Kip Thorne described the singularity as the point where all laws of physics break down.
Another problem with black holes is the black hole information paradox. The issue is that if a particle falls into a black hole information about its state is lost. This is forbidden by the laws of physics as we know them. Stephen Hawking is working on a new theory by which the information is somehow retained at the event horizon.
Clearly we need new laws of physics if we are to completely understand black holes. As nothing which goes past the event horizon can ever escape. This makes it impossible to see inside a black hole.
So, yes, black holes defy the laws of physics as we know them. This means that our laws of physics are incomplete.
In a star if helium fuses to make carbon, what makes the elements in between?

Answer:
The elements Lithium, Beryllium and Boron are made by cosmic rays.
Explanation:
The elements Hydrogen and Helium were made during the Big Bang. Helium is also made by fusion reactions in stars.
The elements Lithium Beryllium and Boron can't be made in any quantity is stars as they are intermediate steps in other fusion reactions. Any of these elements present at the birth of a star will get consumed by later reactions.
These intermediate elements (Lithium, Beryllium and Boron) are produced by cosmic rays. These are high energy protons and other particles. These collide with nuclei of Carbon and Oxygen which breaks them down and produces Lithium, Beryllium and Boron.
Carbon is produced by reactions such as the triple Helium reaction. This reaction explains what happens to Beryllium.
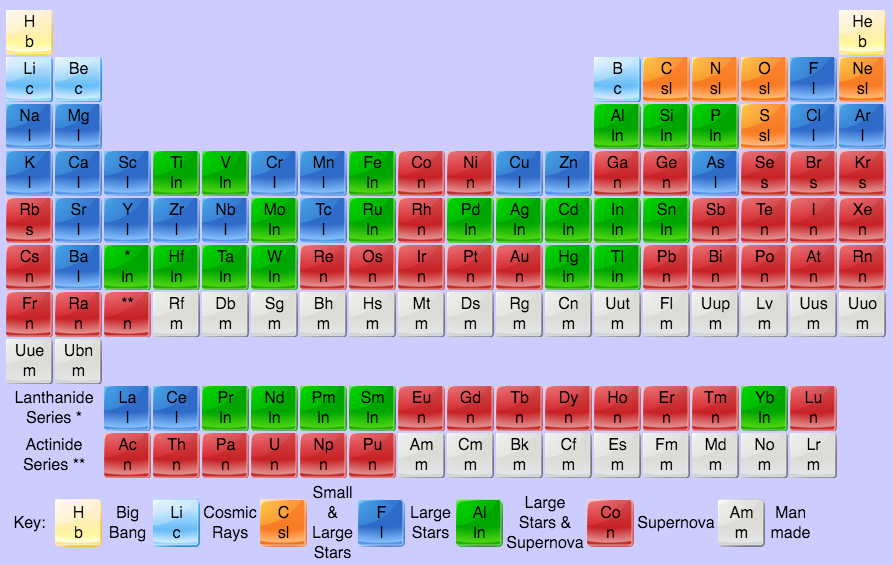
The diagram shows where all of the elements are created.
How do we know about the sun interior?
Answer:
By using mathematical models from what we can measure and observe from the surface.
Explanation:
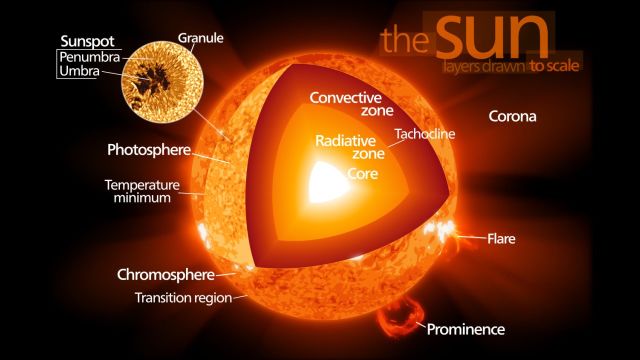
Physicists can't look inside the sun to find out what's there. Instead, they have to do a bit more thinking. By observing the particles and radiation emitted, the motions of gas and something called solar oscillations, we can make models using physics, maths and what we already know about how matter behaves.
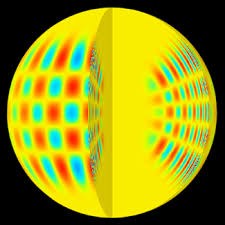
Solar Oscillations - The sun's surface oscillates (moves up and down) due to sound waves that are generated and trapped within the sun's interior. The way that these sound waves are reflected within the sun's atmosphere can tell us a lot about the materials within in, and their nature.

Solar neutrinos - The reactions within the sun emit tiny particles called neutrinos. Unlike photons (light) these can travel from the sun's core to its surface very quickly. By observing these neutrinos, we can tell a lot about the rate of reaction within the sun as well as its pressure, temperature and density.
Then, once you have some data, it's a matter of applying laws and formulae that have been confirmed through measurable experiments on earth to form models.
I hope this helps; let me know if I can do anything else:)
Do astronauts age while traveling in space?

Answer:
Yes - they will experience aging in what they perceive as a normal way. An Earth-based observer will observe an astronaut aging slower or faster depending on various factors discussed below.
Explanation:
Do astronauts age while traveling in space? Let's explore that question.
The first thing to keep in mind is that an astronaut will experience time normally - 24 hours will be experienced as 24 hours (and not something shorter or longer). And so from the astronaut's point of view, s/he will age and age normally.
It's when we start comparing the aging rate to someone in a different location, like an observer on Earth, that things start to get complicated.
There are two ways that time can dilate - that is, that time can be seen to be passing at a slower rate for different observers:
-
High velocity. Einstein's Theory of Special Relativity says that time will dilate (slow down) for someone experiencing high velocity. Astronauts experience a very high velocity compared to an observer on Earth and so the Earth observer will observe that the astronaut ages more slowly.
-
High gravity. Einstein's Theory of General Relativity says that time will dilate for someone in a high gravitational field. Astronauts experience lower gravity than on Earth and so the Earth observer will observe that the astronaut ages more quickly.
I should note that for both of these effects, because we're not working with extreme velocity (a significant fraction of the speed of light) or extreme gravity (such as around a black hole), the effects are quite small. But they are enough that they can be measured and do have effects on everyday life.
So let's talk details.
Special Relativity
Let's take a look at the equation that deals with time contraction while traveling at high speed:
This is Einstein's Special Theory of Relativity, where
For fun, let's ask the question What would it take for an astronaut to not age? Or in other words, what would it take for an observer on Earth to look at an astronaut and observe he is not aging? The answer is the astronaut would have to be traveling at the speed of light:
So no matter the value of
But perhaps an astronaut will age slower in space than on Earth. Let's explore that - first let's start with the equation again:
According to "the internet", the ISS (International Space Station) travels at around
So in a year of traveling on the ISS, an astronaut would be observed to have aged roughly
General Relativity
Einstein also developed General Relativity, which predicts that someone in a gravitational field will age slower than one outside of it. Since our astronaut will be in a lesser gravitational field than the observer on Earth, the astronaut would be observed to be aging faster! But as we can see from the above, the effects are very very slight.
Putting it together
On Earth, we experience time in our "normal" Earth-based way. As we increase in altitude away from the Earth and the gravity we experience decreases, an observer would see us aging faster. Also, as we orbit the Earth (or head off for the Moon or elsewhere) and our velocity increases, an Earth-based observer would see us aging slower. And it turns out there is a point in space where the two effects cancel (thanks for the tremendous work by @phillip-e!). He writes:
The mathematics goes like this. For a satellite in orbit the time dilation due to orbital speed is:
The gravitational time dilation for a distance of
If we need to know at what height the slowing due to speed cancels out the speeding up due to weakened gravity we can compare the
Using Newtonian gravity:
Then:
Divide by
This gives:
So, time passes slower if the satellite, like the ISS, is orbiting lower than an altitude of a half Earth radius, about 3,000 km, and it passes faster if higher, like GPS.
GPS satellites
According to http://metaresearch.org/cosmology/gps-relativity.asp, "For GPS satellites, GR predicts that the atomic clocks at GPS orbital altitudes will tick faster by about 45,900 ns/day because they are in a weaker gravitational field than atomic clocks on Earth's surface. Special Relativity (SR) predicts that atomic clocks moving at GPS orbital speeds will tick slower by about 7,200 ns/day than stationary ground clocks."
(For some reason, the metaresearch link appears to be broken, but this link from the Astronomy Dept. at Ohio State University provides the same analysis and further discusses how it impacts the GPS network: http://www.astronomy.ohio-state.edu/~pogge/Ast162/Unit5/gps.html)
So the net result is that clocks on GPS satellites, clocks will appear to run faster by 38,700 nanoseconds per day, which is .00000387 seconds, or about 122 seconds per year - so about 2 minutes/year.
ISS
The International Space Station, orbits at 400km which is lower than the 3000 km mark and so time for those astronauts passes slower for them than it does on Earth.
Space Missions
But as speeds increase for astronauts heading to the Moon and elsewhere, Special Relativity causes more time dilation. And as gravity decreases, time speeds up... and so the calculations over which prevails will change...
Does the Oort cloud exist? If so, why can't we see it?

Answer:
The Oort Cloud is theorized to exist but due to many factors we can't see it.
Explanation:
First let's talk about what the Oort Cloud is (and what it isn't).
The first thing to know is that it is theorized that the cloud exists. While definitive proof will be difficult to come by, the theory helps explain many questions in astronomy (where do long-period comets come from and how to describe their orbits, etc)
From http://space-facts.com/oort-cloud/, it's a region of space that surrounds the solar system where ice, rock, and the occasional larger body (sometimes called Dwarf Planets) exist. The region is a spherical shell and starts about 2,000 AU (Astronomical Units) from the Sun (and to put that into perspective, 1 AU is the average distance from Earth to the Sun. Pluto is 40 AU from the Sun.) and extends well out towards the closest star (perhaps as much as 100,000AU away from the Sun or roughly 1/4 of the distance between the Sun and the closest star).
What it isn't is a cloud in the sense we think about clouds on Earth - big puffy things made up of water vapour that are easy to spot in the sky. Clouds in the astronomical sense are far less dense but are much more vast so that we see them when the light of stars and galaxies is interfered with.
So what would make the cloud hard to see?
Things that we observe in space are observable only if we can see them.
So what does it take to be able to see something? Light.
And where does the light come from? It either is produced by the object (ex. the Sun, a lamp, etc) or the light is reflected off the object (ex. the Moon).
When light is reflected, all the light that strikes the object doesn't bounce back - it gets scattered, absorbed, and the like, so only a tiny fraction of what strikes the object is reflected back (which is why the Moon, even though it can be quite bright at night, isn't anywhere near as bright as the Sun. The Moon absorbs some light and what is reflected is scattered off in all sorts of directions - only a fraction reaches Earth).
Clouds in the Earth's sky are visible because there is a strong light source (the Sun) that allows the clouds to scatter the light and yet still have plenty left for us to look up and see them. There is no light source like that for the Oort Cloud, so what light it gets, when scattered, doesn't come back towards Earth but instead flies off in random directions.
How much light does the Oort Cloud receive? Light diminishes exponentially with distance. A strong light source at distance 1 will only be
The Oort Cloud does not make its own light, so we need reflected light to see it. The Cloud is made up of small rocks and pieces of ice with huge distances between them, so most of the light that does manage to make it there passes right through and never reflects. Space rocks and ice are notoriously "dirty" - or covered in a dark coloured "space dust", so most of the light is absorbed by the rocks in the Cloud. And the distances involved are massive, so much so that to see Pluto and a few of the other large objects in the Cloud, it takes very powerful telescopes and a lot of luck in finding them.
The only other way of seeing the Cloud is with the use of a deep space probe. However, because of the vast distances, it's difficult to build a spacecraft that can make the journey. According to https://en.wikipedia.org/wiki/Oort_cloud, Voyager 1, the farthest and fastest moving probe we have and launched in 1977, will be another 300 years before it reaches the Cloud and by then will have no power to explore or send back data. Other probes also making their way out of the solar system will also run out of power long before making contact with the Oort Cloud.
Why do astronauts in space experience less gravitational force than they do on earth?

Answer:
As
Explanation:
There are a couple of ways of answering this question: one is to answer your specific question about the force of gravity experienced by an astronaut, and the other is to talk about the weightlessness experienced in space.
Let's first talk gravity:
Gravity is a force that one mass exerts on another mass. The equation for that force is:
where
The question being asked is about the experience of gravity by an astronaut in space. So let's work this out: as a person rises up into the sky, what in the equation is changing?
So as the astronaut rises up above the Earth, the denominator in the equation gets bigger, resulting in less gravitational force the astronaut experiences from the Earth (and coincidentally the Earth experiences less gravity from the astronaut - but the Earth is so massive it hardly notices!)
Ok - so now let's talk about weightlessness:
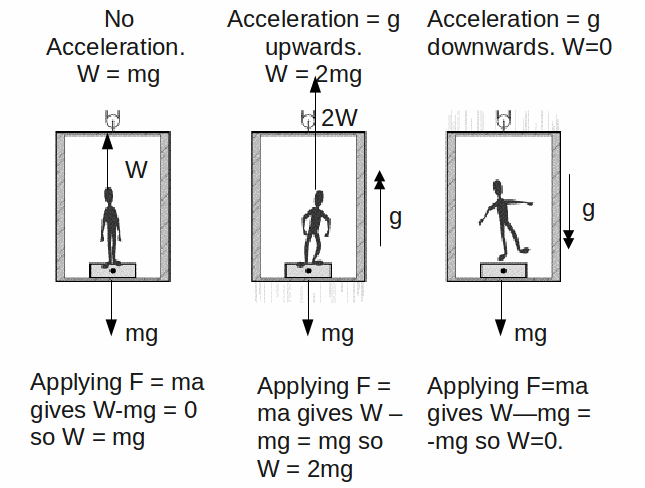
We've seen on TV and youtube and movies how an astronaut in space, say for instance one living aboard the ISS (International Space Station), seemingly floats in midair. They can take a water droplet and play with the little spherical drop and can add more and more water to make the sphere bigger. So - how is this possible? Is it a result of experiencing a lesser amount of gravity? The answer is - partly.
Remember the story about Sir Issac Newton and the apple - how the apple hit him on the head and suddenly he had the framework for the theory of gravity? What's far more likely in that story is that after the apple hit him on the head, he wondered why the Moon didn't do the same thing - why it keeps moving around the Earth and not plummeting onto it.
The answer here is what @SCooke is getting to in his answer: the movement of someone (or something) in orbit is one part falling towards Earth and one part moving tangentially away from Earth, with the two vectors adding up to being a sort of continuous falling - you fall but never land. Everything in orbit, whether the astronaut or the water drop or the Moon, they are all falling towards the Earth but will never hit it. And it's that continual falling that is the experience of weightlessness.
Why are the Jovian planets so much larger than the terrestrial planets?

Answer:
See explanation...
Explanation:
Think of planets forming from the protoplanetary disk around a star.
Gases and dust in the disk are drawn to one another by gravity and coalesce to start to form planets and smaller bodies. As the mass of a planet increases, so does its gravitational pull on the dust and gas molecules through which it passes. Apart from major collisions, each planet eventually more-or-less (*) clears a path through the debris.
During this time of planet formation, the light pressure and solar wind from the star will tend to strip any atmosphere from the forming planets and asteroids, unless they are massive enough to retain it by gravity. In particular lighter elements like hydrogen and helium will only be retained in significant proportion in planets over a certain mass. Once planets have such a mass they will grow considerably, collecting gases from the surrounding disk, while their smaller cousins will tend to stay smaller.
(*) One interesting thing about the orbital path of a planet is that there are
Objects in synchronous orbit near L4 or L5 are known as trojans.
The first such object detected in the case of the Earth Sun orbit was the asteroid