Make the internet a better place to learn
What is the LCM of 10, 15, 20 and 30?

Answer:
Explanation:
First, write out the prime factorization of each number
#10 = 2 xx 5# #15 = 3 xx 5# #20 = 2^2 xx 5# #30 = 2 xx 3 xx 5#
We can rewrite the above with more clarity as
#10 = 2^1 xx 3^0 xx 5^color(blue)(1)# #15 = 2^0 xx 3^color(blue)(1) xx 5^color(blue)(1)# #20 = 2^color(blue)(2) xx 3^0 xx 5^color(blue)(1)# #30 = 2^1 xx 3^color(blue)(1) xx 5^color(blue)(1)#
For each prime factor, take the one with the highest exponent. 2 is raised to the power of 2 in 20. 3 and 5 have both a maximum exponent of 1. Refer to the
Therefore,
#"LCM" = 2^2 xx 3^1 xx 5^1#
#= 60#
This algorithm is guaranteed to generate the least common multiple.
What is #6.73-2*5^0-:2#?

Answer:
Explanation:
#6.73-2*color(teal)(5^0)-:2#
#=6.73-2*color(teal)1-:2#
#=6.73-color(darkorange)(2*1)-:2#
#=6.73-color(darkorange)2-:2#
#=6.73-color(violet)(2-:2)#
#=6.73-color(violet)1#
#=color(green)(|bar(ul(color(white)(a/a)color(black)(5.73)color(white)(a/a)|)))#
Craig is folding laundry for his family. In the basket, #1/6# of the shirts belong to his older brother and #3/6# of the shirts belong to his younger brother. What fraction of the shirts belong to either his older or younger brother?

Answer:
Explanation:
Given:
- Craig's older brother's shirts take up
- Craig's younger brother's shirts take up
You are trying to find:
- how much of the basket belongs to Craig's older or younger brother
Thus, add
#1/6+3/6#
#=(1+3)/6#
#=4/6#
Since the numerator and denominator have a common factor of
#(4color(red)(-:2))/(6color(red)(-:2))#
#=color(green)(|bar(ul(color(white)(a/a)2/3color(white)(a/a)|)))#
What is 29 degrees celsius in fahrenheit?

Answer:
Explanation:
The numbers to remember are 5, 9 and 32
Fahrenheit are the lager number when comparing like temperature for like. So to convert Centigrade to Fahrenheit, you need to make the numbers bigger. Thus you multiply by
All you need to remember now is that freezing point for each is different.
Centigrade freezing point is
Fahrenheit freezing point is
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
We are going from Centigrade to Fahrenheit so it is small number to large. So we have
We are changing freezing point from 0 on 1 scale to 32 on a different scale so we now have:
Thus the full conversion is:
Bob is training for a race. Bob ran 14.6 miles away from his home. Then, Bob ran 9.8 miles towards his home Finally, Bob ran 5.3 miles away from his home. How far is Bob from his home?

Answer:
Explanation:
Bob's training can be broken down into three steps:
#1# . ran#14.6# miles away from home
#2# . ran#9.8# miles towards his home
#3# . ran#5.3# miles away from his home
Since Bob starts running from his home, he is
If he starts running from his home for
#0color(white)(i)"miles"+14.6color(white)(i)"miles"#
When Bob runs towards his home at a distance of
#0color(white)(i)"miles"+14.6color(white)(i)"miles"-9.8color(white)(i)"miles"#
Finally, when Bob runs
#0color(white)(i)"miles"+14.6color(white)(i)"miles"-9.8color(white)(i)"miles"+5.3color(white)(i)"miles"#
If you solve the addition problem, you get
What is the divisibility rule for 11, 12, and 13?
Answer:
Please see below.
Explanation:
Divisibility Rule for
Divide the alternate digits in two different groups. Take the sum of alternate digits separately and find the difference of the two numbers. If the difference is
Example:
Divisibility Rule for
If the number is divisible by both
Example: In
Divisibility Rule for
Recall the divisibility rule of
Starting from right mark off the digits in groups of threes (just as we do when we put commas in large numbers).
Now add up alternate group of numbers and find the difference between the two. If the difference is divisible by
For example
and
As difference between
As
How can you convert a decimal to fraction?

Answer:
See explanation...
Explanation:
If it is a terminating decimal, then multiply it by a power of
For example:
#0.16 = 16/100 = (color(red)(cancel(color(black)(4)))*4)/(color(red)(cancel(color(black)(4)))*25) = 4/25#
If it is a repeating decimal, then multiply by a power of
For example:
#0.2345345345... = 0.2bar(345)#
Multiply by
#(10000-10)0.2bar(345) = 2345.bar(345) - 2.bar(345) = 2343#
So, dividing by
#0.2bar(345) = 2343/(10000-10) = 2343/9990 = (color(red)(cancel(color(black)(3)))*781)/(color(red)(cancel(color(black)(3)))*3330) = 781/3330#
What is 25% of 90?

Answer:
25% of 90 is 22.5.
Explanation:
A percent is any number over 100, so 25% is 25 over 100, this means that 25% can be written as:
Now, any number in fractional form (a number over a number) is the same as division so 25% can also be written as a decimal, we just move the decimal point 2 places to the right of 25, like this:
Now we have two ways that we can solve this problem! I'll start with the fractional method of solving.
---------------------------
The Fractional Method
So we have a fraction:
and
so that means,
or
This means that we need four 25's to get 100.
or,
(we could also divide both numerator and denominator by 5 to get the same result:
Now that we know 25% is equal to
---------------------
The Decimal Method
As we found out above 25% equals 0.25 so we can solve this problem using decimals too! All we need to do is multiply 90 by 0.25, which gives us the same answer as above.
---------------------
Despite the fact that that mathematics seemed to be a lot more involved in the fractional method, the calculations were a lot easier and personally I found it to be faster than the decimal method. The decimal method is great when you're working with fractions that aren't equal to 100 (For example:
Sorry this is so long, I hope it helped though!
What is -3/10 as a decimal?

Answer:
Explanation:
So lets first operate with positive numbers. We should go about this by thinking about a pie, like this:
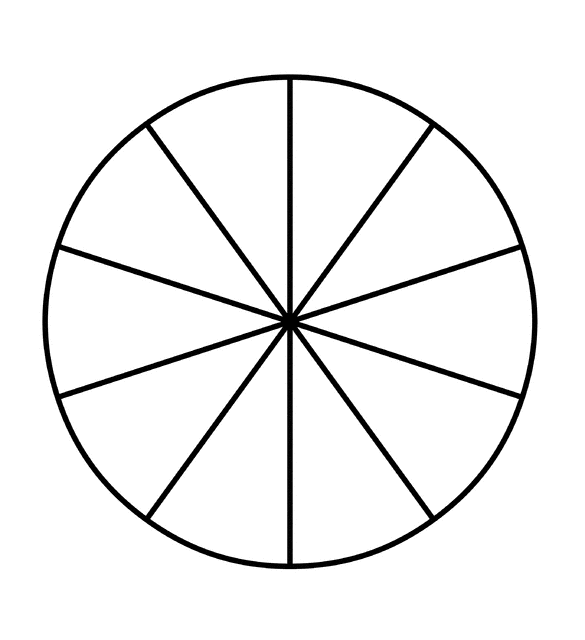
Courtesy of: http://etc.usf.edu/clipart/40600/40610/pie_01-10a_40610.htm (ClipArt ETC Free Classroom License)
Lets say that the circle above is an apple pie. The apple pie has 10 slices, or parts. If no one takes a piece of the pie then we have all 10 slices of the pie. Since we have all ten slices of pie we can say that we have "10 of the 10 slices" or
...or a full pie (this is sweet potato pie):

Courtesy of: http://culinaryphysics.blogspot.com/2015/11/patti-labelle-sweet-potato-pie-recipe-soul-food.html (Public Domain)
Or this (key lime):

My own photo (and baking), feel free to reuse, if you want the recipe shoot me a message
Okay, now lets say that 9 people enter the room and they all take a slice of the pie. That means there is only on piece of pie left
We know this because
There's an underlying tend here, which looks like this:
_______
_______
_______
_______
_______
_______
_______
_______
_______
_______
This exact same trend exists for negative fractions we just have to put a negative sign in front of the decimal. This means that:
I hoped this helped!
Which operation should be performed first according to the order of operations of #44-:2 + 9 - [120 - (5 + 10 *7)]#?
Answer:
First you have to multiply
Explanation:
When talking about order of operation the PEDMAS rule applies. According to this rule first you have to calculate everything which is in the most inner brackets.
In this expression you have 2 kinds of brackets, but it makes no difference how they look like because you only have to look at those which contain no other brackets, and they are
In those brackets you have 2 operations: addition and multiplication. According to PEDMAS rule you have to do multiplication first, then the addition, so you get:
In every line the next operation is marked with the red color exept last line with only one operation (substraction