Make the internet a better place to learn
How do I sum the series sum_(n=1)^oon(3/4)^n?

The answer is: 12.
First of all: "How much is the sum of a geometric series?".
Let's list all the terms of the series:
or, better:
The first sum is:
The second sum is:
The third sum is:
The fourth sum is:
So:
Water is leaking out of an inverted conical tank at the rate of 10,000cm^3/min cm/min at the same time that water is being pumped into the tank at a constant rate. The tank has a height of 6m and the diameter at the top is 4m. If the water level is rising at a rate of 20 cm/min when the height of the water is 2m, how can I find the rate at which water is being pumped into the tank.?
Answer:
(see below for solution method)
Explanation:
Start by ignoring the leakage and determine the rate of inflow required to achieve the specified rate of height (depth) of water increase.
Later we'll use the fact that
Actual inflow rate
= Inflow Rate for Increased Depth + Leakage Rate
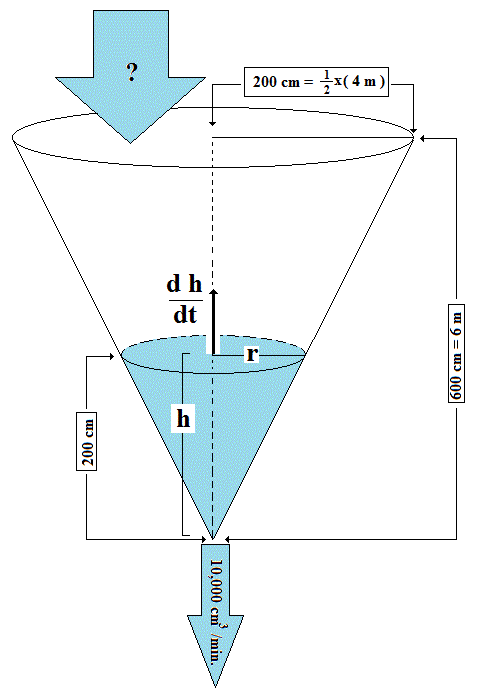
For the given cone the ratio of r adius to h eight is
so
The formula for the volume of a cone:
We are interested in the change in Volume with respect to time and note that
Using the value we've already calculated for
we get:
or roughly
This is the Inflow Rate Required to Cause Height Increase and
ignores the Rate of Leakage
The Actual Inflow Rate needs to be the sum of these two:
How do you find f ' if f(x)=sin (1/x^2)?

Answer:
An interesting example related to this one is to consider the piecewise-defined function
Explanation:
Again, let
Certainly, when
But
In other words,
Here's a graph of the function
Pretty amazing, isn't it?!?!
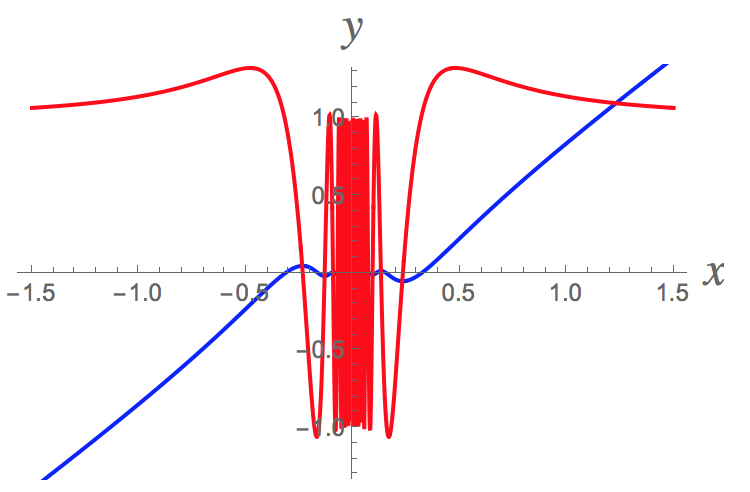
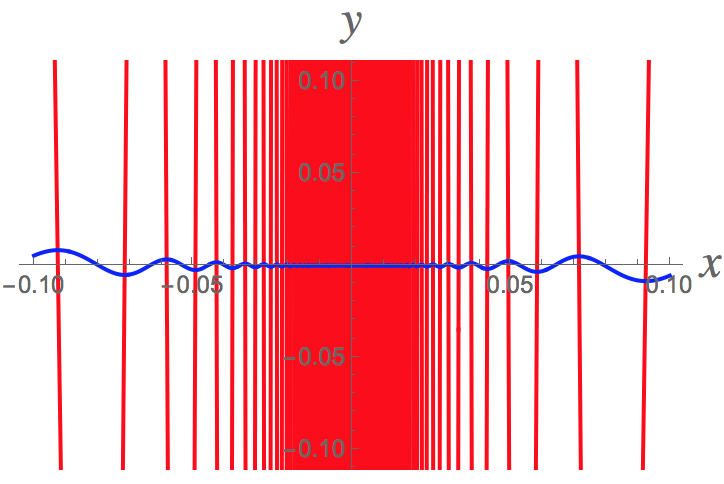
Here a closer view near the origin and also making sure we can still see the blue curve. It's oscillating infinitely often as
How do you use the Squeeze Theorem to find lim Sin(x)/x as x approaches zero?

Answer:
For a non-rigorous proof, please see below.
Explanation:
For a positive central angle of

Source:
The geometric idea is that
So we have:
For small positive
So
so
We also have, for these small
so
Since both one sided limits are
Note
This proof uses the fact that
That fact can be proved from the fact that
Which can be proved using the squeeze theorem in a argument rather like the one used above.
Furthermore: Using both of those facts we can show that the sine and cosine functions are continuous at every real number.
Can a point of inflection be undefined?

Answer:
See the explanation section below.
Explanation:
A point of inflection is a point on the graph at which the concavity of the graph changes.
If a function is undefined at some value of
However, concavity can change as we pass, left to right across an
Example
The concavity changes "at"
But, since
graph{1/x [-10.6, 11.9, -5.985, 5.265]}
Example 2
The second derivative is undefined at
But, since
graph{x^(1/3) [-3.735, 5.034, -2.55, 1.835]}
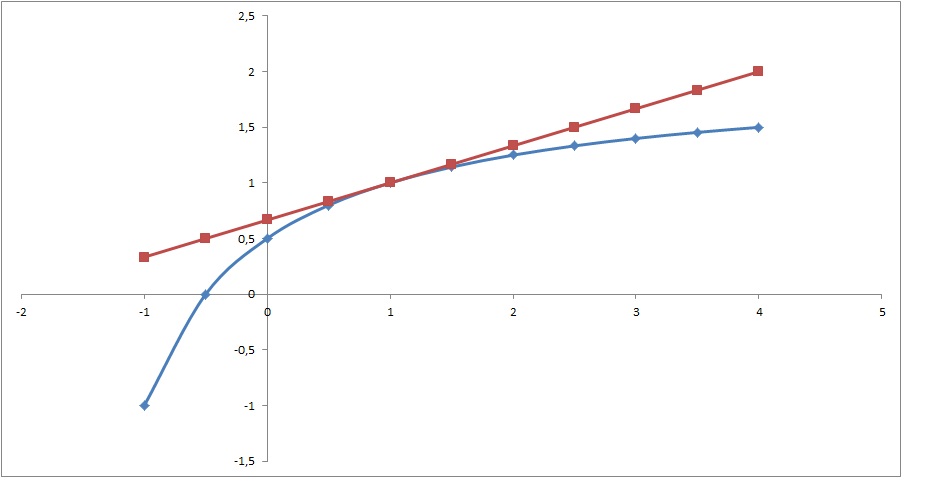
For f(x)=(2x+1)/(x+2) what is the equation of the tangent line at x=1?

Answer:
I found:
Explanation:
First you need to find the slope
at
Now we need the
The equation of a line passing through
Graphically:
What is the derivative of arc csc(sqrt(x+1))?

Answer:
Explanation:
To evaluate inverse trigonometric functions, a valuable technique is implicit differentiation:
In this case, we also will use the chain rule:
as well as the following derivatives:
Now, let
Through implicit differentiation:
And through the chain rule
So
But we want our final answer entirely in terms of
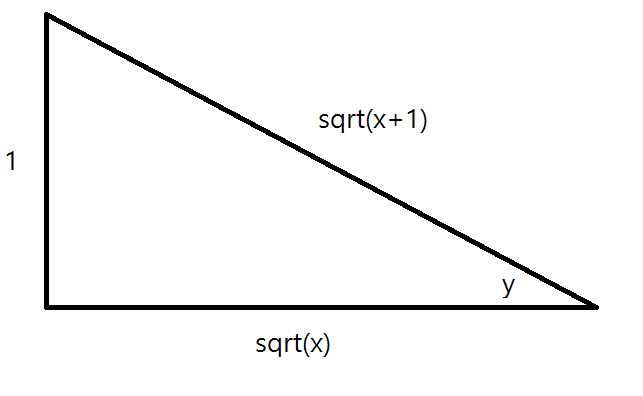
From this we can see that
Thus we have
From this, we can get our final answer
How do you find int (x^2) / (x^2 -3x +2) dx using partial fractions?

Answer:
1) make sure that the degree of your denominator is greater than the degree of your numerator
2) factorize the denominator
3) perform the partial fraction decomposition
4) solve the integral!
Solution:
Explanation:
1) Check degrees of denominator and numerator
First of all, you can't immediately start building partial fractions since the degree of your numerator is equal to the degree of your denominator (the strongest power in both expressions is
However, the partial fraction decomposition will only work if the degree of the denominator is greater than the degree of the numerator.
If the expression was more complicated, normally, at this point, a polynomial division is in order. Here we can achieve the goal in an easier way:
So, now we can build the partial fractions decomposition of the latter fraction.
2) Complete factorization of the denominator
To do so, let's factorize the denominator completely first:
[You can do so by setting
3) Partial fraction decomposition
So, our goal is to find
First, multiply both sides of the equation with
To find the solution of this equation, we need to "collect" the
The solution of this linear equation is
So, our partial fraction decomposition is:
In total:
4) Solving the integral
The last thing left to do is solve the integral!
Hope that this helped!
How do you differentiate f(x)=cose^(4x) using the chain rule.?

Answer:
Explanation:
Your chain can be defined as follows:
Thus, to compute the derivative, you need to build the derivatives of
Now, the only thing left to do is to multiply the three derivatives!
Why is d/dxe^x=e^x?

Answer:
The "why" depends on how you've defined
Explanation:
Define
One approach is to define
then to define
finally, define
In this case
Differentiating implicitly gets us
So,
Define
Definition 1
For positive
(We owe you a proof that this is well-defined.)
Then, using the definition of derivative:
We then define
With this definition we get
= e^xlim_(hrarr0)((e^h-1)/h) = e^x
Definition 2
(
(We owe you a proof that this is well defined.)
Differentiating term by term (we owe you a proof that this is possible), we get
Which simplifies to