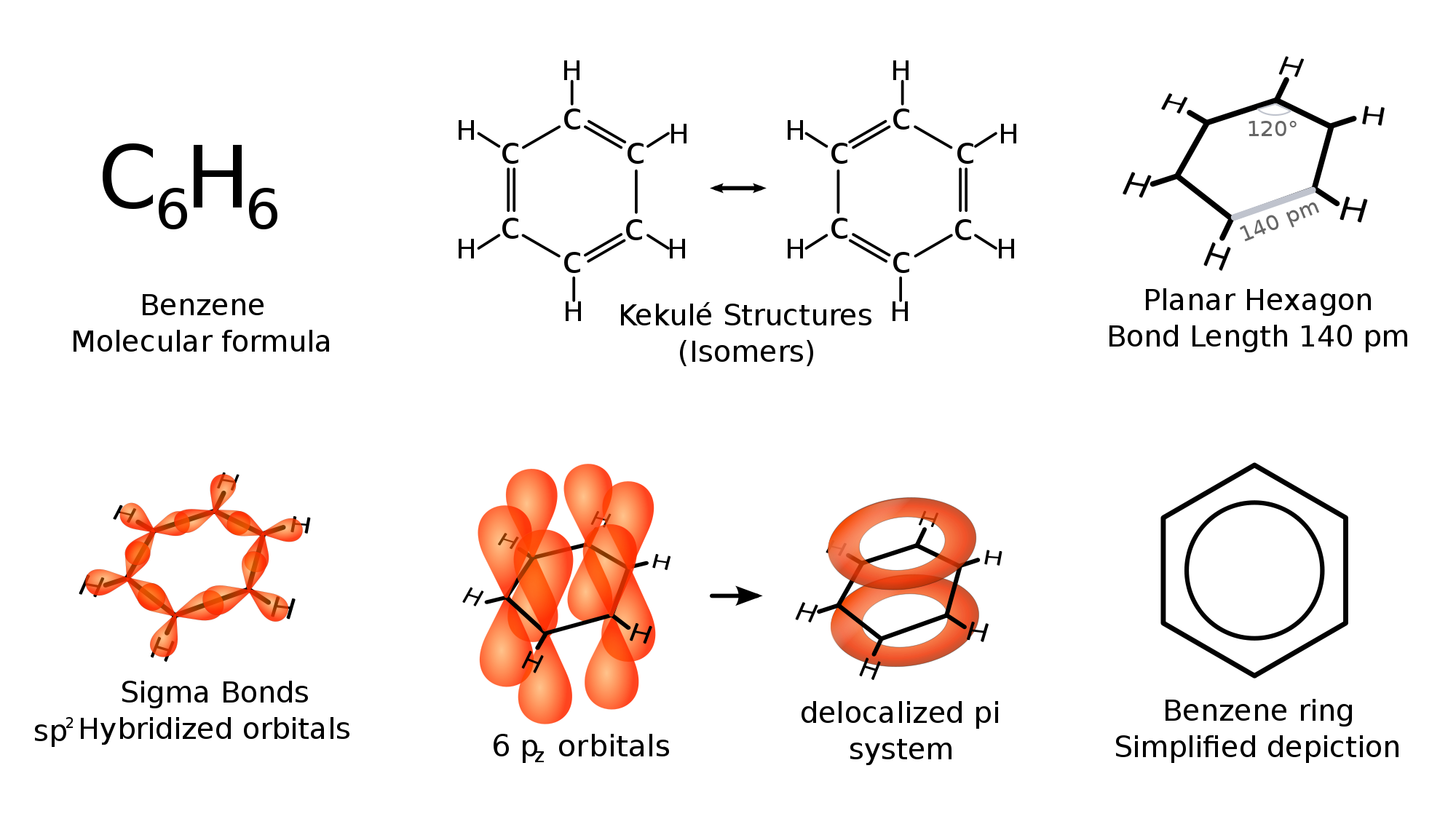Make the internet a better place to learn
How many resonance structures can be drawn for ozone?

Ozone, or
The total number of valence electrons the ozone molecule has is equal to 18 - 6 electrons from each oxygen atom. The two possible Lewis structures that can be drawn for ozone are
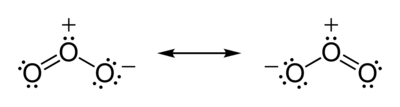
Both structures account for the needed 18 valence electrons - 6 from 3 bonds and 12 as lone pairs placed on the oxygen atoms. The two structures are equivalent from the stability staindpoint, each having a positive and a negative formal charge placed on two of the oxygen atoms.
As a result, both structures will contribute equally to the overall hybrid structure of the molecule, which can be drawn like this

The hybrid structure, shown above on the right, will have two (-1/2) partial negative charges on two of the oxygen atoms and a positive (+1) charge on the third one.
The molecule's
Other resonance structures can be drawn for ozone; however, none of them will be major contributors to the hybrid structure. Here are two more possible resonance structures
These structures will be very minor contributors because, most importantly, both have an oxygen atom that lacks a full octet, and because there are fewer covalent bonds present compared with the other two structures, another factor that significantly decreases structure stability.
So, as a conclusion, ozone has two resonance structures that are major contributors to its hybrid structure, and at least two more that are very minor contributors.
What is mass spectrometry (MS)?

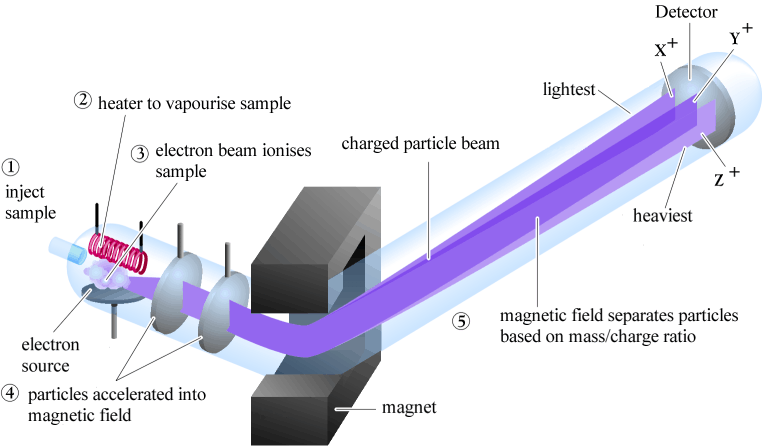
Mass Spectroscopy (MS), in the most basic sense, is for tracing the fragmentation patterns of molecular ions in order to identify them. This tends to be more useful when coupled with other processes, such as Gas Chromatography and Liquid Chromatography.
MS has an interesting process by which we do the following (in a vacuum):
- Inject liquid sample (might be a few
#muL# if you are injecting into a GC-MS setup; depends on the injection method) - Vaporize sample (must be a gas to minimize undesirable fragmentation)
- Ionize sample (must be an ion to interact with electric/magnetic fields) to facilitate fragmentation
- Accelerate fragments into field (electric and/or magnetic) to separate ions by
#m/z# ratio - Detect the ions to get a count for the abundance of each ion
- Acquire mass spectrum
This is the essential process of Mass Spectroscopy.
In further depth:
Inject the sample via some method, such as the 30-ft long tube you use in Gas Chromatography (i.e. the GC is interfaced with MS and you have a GC-MS setup), for example.
Some sort of sample vaporization occurs so that you have a gaseous sample. This may be done with, perhaps, a coil with electric current flowing through it, or maybe a hot flame (
Some sort of ionization occurs (which facilitates fragmentation), such as:
- Chemical Ionization (soft/indirect ionization via the presence of ions in the system)
- Matrix-Assisted Laser-Desorption Ionization (a sample matrix is hit with a laser, ionized, and the matrix itself soft-ionizes the sample embedded within and shielded by the matrix)
- Electron "Impact", where an electron beam allows electrons to interact with the sample to knock off an electron and thus ionize it (hard ionization).
The point of having both soft and hard ionization is that soft ionization better-retains the parent peak during fragmentation, so that you can find the peak that corresponds to the molecular mass of the original ion.
The fragments are then accelerated into an electric and/or magnetic field for the purpose of separating it by a mass-to-charge ratio,
The ions must reach a detector, such as a Faraday Plate or Faraday Cup. Behind it would be some sort of transducer to convert/encode the number of ions that are counted into a current that acts as a signal for a computer to read, so that it can generate some sort of display to give you your mass spectrum.
Why is the #C_6H_8# molecule different from benzene with respect to resonance?

Answer:
Benzene has two important equivalent resonance contributors, while any other
Explanation:
There are many molecules with the formula
Benzene
Benzene has two equivalent resonance contributors, neither of which involves the separation of charge.
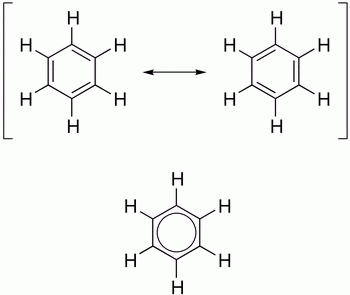
(from chemistry.stackexchange.com)
Hexa-1,3,5-triene
Hexa-1,3,5-triene has only one important resonance contributor.

(from www.chemsynthesis.com)
Any other contributor we might draw has a separation of charge. For example,
Cyclohexa-1,3-diene
Cyclohexa-1,3-diene is an "almost"-benzene.

But it is still a "linear" diene.
Like hexa-1,3,5-triene, it has only one important resonance contributor, with any other contributors having separation of charge.
Question #24d0b

Answer:
benzene does not have any double bonds
Explanation:
benzene or C6H6 does not have any double bonds. but instead it has bonds which falls between double and single bonds
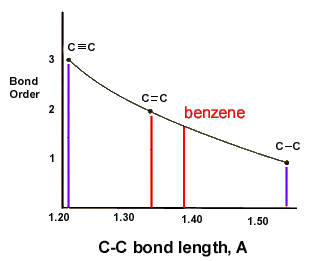
The scientist Kekule proposed that benzene has two resonance structures which has three double bonds each. but later, according to the molecular orbital theory and hybridization, it was discovered that the real structure of benzene is almost similar to the resonance hybrid of the 'Kekule' structures.
take a look at the following images which explains the bonding of C atoms in benzene
Question #16819

Answer:
(a):
Explanation:
The configurations of each stereocentre is depicted in the scheme below:

(a):
1- Assign priorities by decreasing atomic number. For example,
2- For both stereocentres the rotation is counter clockwise; therefore, their configurations are
(b):
1- Assign priorities as explained in (a).
2-
3-
(c):
1- Assign priorities as explained in (a).
2-
3-
Here are two videos that explain in details how to label stereogenic centres R or S:
What are major resonance structures?

WHAT IS A MAJOR RESONANCE STRUCTURE?
The most stable structural "snapshots" of a molecule's electron distribution is its major resonance structure. Let's suppose that we examine the resonance structures of urea,
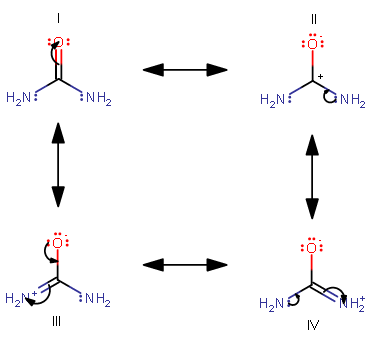
The curved arrows indicate the movement of electrons that lead to a new resonance contributor. We start at I and continuously move clockwise.
FORMAL CHARGES & ELECTRONEGATIVITIES
First, see how structures III and IV do not have minimized formal charges? Although there is net charge cancellation, nitrogen, being less electronegative than oxygen, tends less to pull electrons towards it; therefore, the major (most stable) resonance structure gives the most electron density to oxygen.
That means I is the major resonance contributor. That automatically means III and IV are the minor resonance contributors (second-most stable).
DEGENERACIES
Also, notice how structures III and IV are actually identical; just reflect them along a vertical axis and they are the same. Those would be known as degenerate structures, i.e. structures that have the same energy as each other.
#E_"III" = E_"IV"#
OCTET RULE
Finally, see how structure II leaves carbon without an octet? You may have learned that atoms prefer to satisfy the octet rule.
Because of a lack of that here, structure II is the most minor resonance contributor (least stable) of these four.
STABILITY & RESONANCE CONTRIBUTIONS
In the end, we have this spectrum of stabilities and resonance contributions:
I > [III = IV] > II
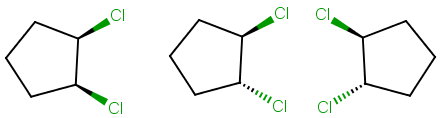
How many stereoisomers are possible for 1,2-dichlorocyclopentane?

Answer:
There are three stereoisomers for 1,2-dichlorocyclopentane.
Explanation:
Here's the procedure I would follow.
- Draw the bond-line structure.
- Identify the chiral centres.
- Calculate the maximum number of possible stereoisomers.
- Draw them.
- Eliminate any meso compounds.
1. Bond-line structure
The bond-line structure is
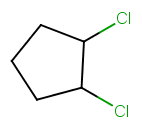
2. Chiral centres
3. Maximum number of stereoisomers
There are two chiral carbons, so the maximum number of stereoisomers is
4. Possible stereoisomers
Draw "UpUp" and its mirror image, then "UpDown" and its mirror image.
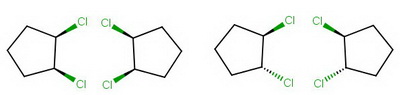
5. Identify meso compounds
Hence there are only three stereoisomers of 1,2-dichlorocyclopentane.
Why is ether used as the solvent during Grignard reactions?

Answer:
Ether is used as a solvent because it is aprotic and can solvate the magnesium ion.
Explanation:
A Grignard reaction involves the reaction of an alkyl (or aryl halide) with magnesium metal to form an alkylmagnesium halide.
Diethyl ether is an especially good solvent for the formation of Grignard reagents for two reasons.
(a) Ether is an aprotic solvent
The
The Grignard carbon is highly basic and reacts with the acidic protons of polar solvents like water to form an alkane.
Ether has no acidic protons, so Grignard reagents are stable in ether.
(b) Ether is a great solvating agent
The
Hence, it is difficult to form a Grignard reagent in a nonpolar solvent.
The
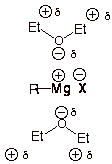
Thus, Grignard reagents are soluble in ether.
What was the first demonstration of organic total synthesis?

Answer:
The first total synthesis was the Finnish chemist Gustav Komppa's total synthesis of camphor.
Explanation:
In 1903, Komppa succeeded in synthesizing camphoric acid from diethyl oxalate and diethyl β,β-dimethylglutarate.
A few years earlier, Haller and Blanc had converted camphoric acid to camphor, so this constituted a total synthesis of camphor.
At the time, camphor was a scarce natural product with a worldwide demand.
Komppa realized this and began industrial production of camphor in 1907.
For the terminally curious, here's a summary of the steps.
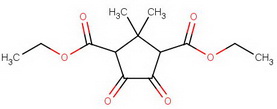
diethyl diketocamphorate (I)
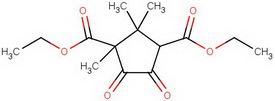
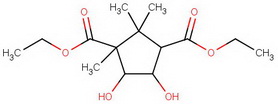
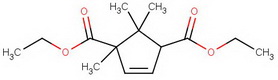
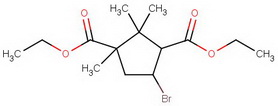
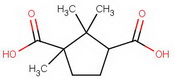
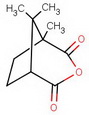
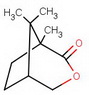
#"KCN"#
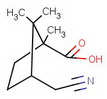
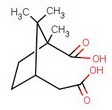
Which is more highly regioselective: a reaction of an alkene with #BH_3# or with #9-BBN#?

Answer:
Explanation:
Hydroboration involves the addition of a
It is often followed by oxidation with alkaline hydrogen peroxide to form an alcohol.

The reaction is regioselective, with the
The regioselectivity is enhanced if a bulky dialkylborane,
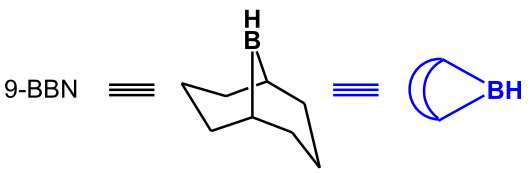
(from http://www.hull.ac.uk/php/chsanb/alkenes/boron.pdf)
In equations, it is often written as the blue shorthand symbol.
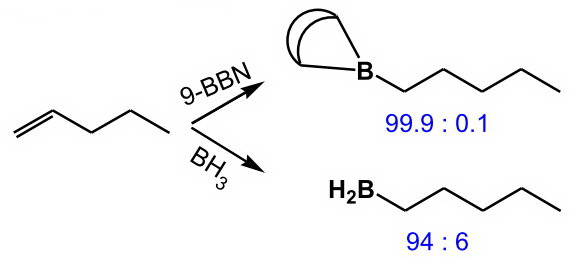
(from http://www.hull.ac.uk/php/chsanb/alkenes/boron.pdf)
This sensitivity to steric effects arises because the rigid bicyclic structure prevents internal rotation to relieve steric hindrance in the transition state.
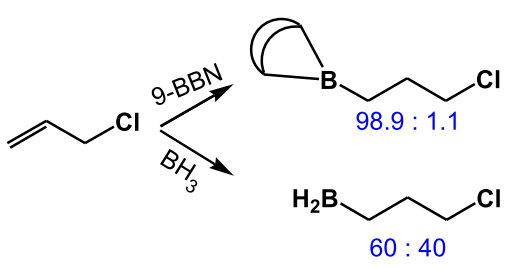
(from http://www.hull.ac.uk/php/chsanb/alkenes/boron.pdf)